Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 33.1 - Ex. 40
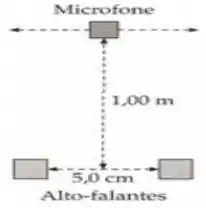
Dois pequenos alto-falantes estão separados por uma distância de 5,0 cm, como mostrado na Figura 33-44. Os alto-falantes são acionados em fase com um sinal de onda senoidal de frequência 10 kHz. Um pequeno microfone é colocado a uma distância de 1,00 m dos alto-falantes no eixo que passa pelo meio dos dois e o microfone é, então, movido perpendicularmente ao eixo. Onde o microfone registra o primeiro mínimo e o primeiro máximo do padrão de interferência dos alto-falantes? A velocidade do som no ar é 343 m/s.
Passo 1
Meus amigos e minhas amigas!
O diagrama abaixo esquematiza toda a questão, mostrando os dois auto-falantes, e a posição inicial e final do microfone. Para resolver, vamos aplicar interferências construtivas e destrutivas e, também, usar a geometria formada pelos auto-falantes e o microfone para encontrar as distâncias onde ocorrem a interferência mínima e a interferência máxima.
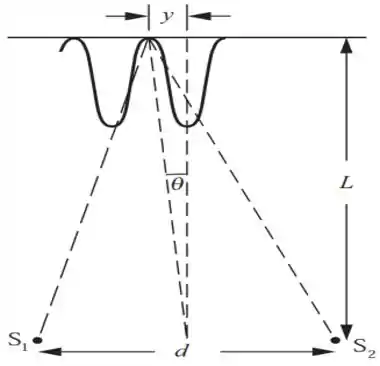
Fazendo, unicamente, a análise do diagrama, constatamos que:
Vamos definir a equação onde ocorrerá a interferência máxima e mínima:
Onde:
E
Seguindo:
Com:
Por fim:
Então, a equação geral será dada por:
Passo 2
Vamos encontrar o primeiro mínimo.
Como descrevemos anteriormente:
Aplicando os valores fornecidos pela questão:
Passo 3
Vamos encontrar o primeiro máximo.
Como descrevemos anteriormente:
Aplicando os valores fornecidos pela questão: