Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 9.1 - Ex. 1
Dois pontos pertencem a um disco que gira, com velocidade angular crescente, em torno de um eixo fixo que passa perpendicularmente pelo centro do disco. Um ponto está na borda e o outro ponto está a meio caminho entre a borda e o centro. (a) Qual dos pontos percorre uma distância maior em dado tempo? (b) Qual dos pontos varre o maior ângulo? (c) Qual dos pontos tem a maior rapidez? (d) Qual dos pontos tem a maior rapidez angular? (e) Qual dos pontos tem a maior aceleração tangencial? (f) Qual dos pontos tem a maior aceleração angular? (g) Qual dos pontos tem a maior aceleração centrípeta?
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Temos dois pontos sobre um disco que gira com velocidade crescente. Eles estão nessas posições:
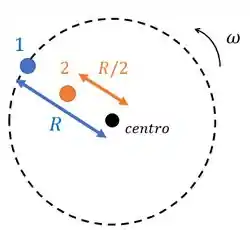
Vamos usar essa imagem para analisar nossos itens. Bora lá!
Passo 2
Item (a): Ele quer saber qual ponto percorre maior distância.
A distância percorrida pelo ponto 1 é o comprimento da borda do disco, certo? Se a gente disser que o disco tem raio , a distância percorrida é
Já para o ponto 2, temos também uma trajetória circular, mas o raio da trajetória é menor e vale , assim a distância percorrida é
Assim, vemos que o ponto na borda percorre uma maior distância, pois possui um raio de giração (raio da trajetória) maior.
Passo 3
Item (b):
Então, se o disco der uma volta completa em torno do eixo, nossos dois pontos voltam a mesma posição da nossa imagem, certo?
Ou seja, se o disco gira um ângulo , todos os pontos vão sofrer esse mesmo deslocamento angular.
Então, a gente pode dizer que os dois pontos varem a mesma angulação.
Passo 4
Item (c):
Cara, a rapidez de um ponto sobre um disco que roda é dada por
Onde é o raio da trajetória (raio de giração) e é a rapidez angular que é igual para todos os pontos no disco.
Então o que a gente precisa fazer é comparar são os raios de giração. Quanto maior o raio, maior a rapidez. O ponto na borda tem raio e de dentro tem raio .
Assim o ponto na borda tem maior rapidez, pois possui um raio de giração maior.
Passo 5
Item (d):
Como falamos antes, todos os pontos tem a mesma rapidez angular. Por que? A rapidez angular é dada por
Ou seja, é a taxa de variação do deslocamento angular .
Já que o deslocamento angular é o mesmo para todos os pontos do disco, a variação desse deslocamento em relação ao tempo também vai ser a mesma.
Então os dois pontos possuem a mesma rapidez angular.
Passo 6
Item (e):
Cara, a aceleração tangencial de um ponto sobre um disco que roda é dada por
Onde é o raio da trajetória (raio de giração) e é a aceleração angular que é igual para todos os pontos no disco.
Então o que a gente precisa comparar são os raios de giração. Quanto maior o raio, maior a aceleração tangencial. O ponto na borda tem raio e de dentro tem raio .
Assim o ponto na borda tem maior aceleração tangencial, pois possui um raio de giração maior.
Passo 7
Item (f):
Como falamos antes, todos os pontos tem a mesma rapidez angular , né? E quem é a aceleração angular? É a taxa de variação da rapidez angular:
Já que a rapidez angular é a mesma para todos os pontos do disco, a variação dessa rapidez em relação ao tempo também vai ser a mesma.
Então os dois pontos possuem a mesma aceleração angular.
Passo 8
Item (g):
A aceleração centrípeta é aquela que tem essa fórmula:
Mas a gente viu que a rapidez vale:
Vamos substituir isso ali em cima:
Onde é o raio da trajetória (raio de giração) e é a rapidez angular que é igual para todos os pontos no disco.
Então o que a gente precisa comparar são os raios de giração. Quanto maior o raio, maior a aceleração centrípeta. O ponto na borda tem raio e de dentro tem raio .
Como o ponto da borda que possui maior raio, possui a maior aceleração centrípeta.
Resposta
a) o da borda, b) ambos varrem o mesmo ângulo, c) o da borda, d) ambos tem a mesma rapidez angular, e) o da borda, f) ambos tem a mesma aceleração angular, g) o da borda