Dois pontos A e B na superfície da Terra estão na mesma longitude e 60,08 separados em latitude, como mostrado na Figura P13.48. Suponha que um terremoto no ponto A crie uma onda P que alcança o ponto B viajando diretamente através do corpo da Terra a uma velocidade constante de 7,80 km/s. O terremoto também irradia uma onda de Rayleigh que viaja a 4,50 km/s. Além das P e S, ondas de Rayleigh são um terceiro tipo de onda sísmica que percorre a superfície da Terra, e não através do corpo da Terra. (a) Qual destas duas ondas sísmicas chega em B primeiro? (b) Qual é a diferença de tempo entre a chegada destas duas ondas em B ?

A distância percorrida pela onda P, , indicada na figura a seguir:

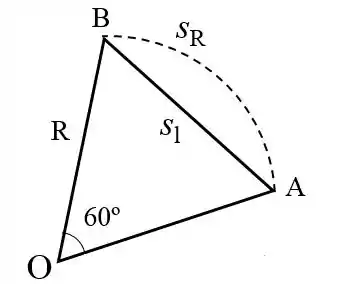
Forma um triangulo equilátero com o raio da Terra, já que o ângulo indicado é de 60° e a soma dos ângulos internos de um triângulo é de 180°, ou seja, todos os ângulos do triângulo formam 60° e, consequentemente, todos os lados são iguais, portanto:

1. A onda P leva um tempo para ir do ponto A ao ponto B:

Enquanto que a onda de Rayleigh leva um tempo

Assim, pode se calcular a diferença entre os tempos de chegada dessas ondas,

(b) Como R é uma constante positiva (R>0), então, concluímos que:

Ou seja, podemos concluir que a onda P é a primeira a ser detectada.

Sendo o raio médio da Terra , então, de acordo com a equação anterior, a diferença de tempo na chegada das ondas é de aproximadamente 665 s.