Usando o fato de que o vetor que representa uma superfície fechada é zero, prove que duas superfícies que têm a mesma linha fechada como contorno são representadas pelo mesmo vetor.

E aí, beleza?? Considere as duas superfícies a seguir, delimitadas pela mesma linha fechada:

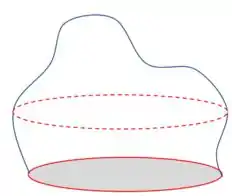
Seja o vetor que representa a superfície à esquerda, o vetor que representa a superfície da direita e o vetor que representa a superfície da linha fechada que delimita ambas as superfícies.

Sabendo que o vetor que representa uma superfície fechada é zero, vem:

Portanto:

Como queríamos demonstrar.