Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 10.Problemas Adicionais - Ex. 114

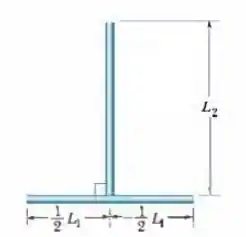
Duas barras finas (ambas de massa 0,2 k g ) estão unidas para formar um corpo rígido como mostra a figura abaixo. Uma das barras tem comprimento L 1 = 0,4 m e a outra tem comprimento L 2 = 0,5 m . Qual é o momento de inércia deste corpo rígido em relação

( a ) Um eixo perpendicular ao plano do papel passando pelo centro da barra menor e

( b ) um eixo perpendicular ao plano do papel passando pelo centro da barra maior?

Passo 1

Olá pessoal, tudo bem? Vamos praticar o cálculo do momento de inércia?

Para calcular o momento de inércia devemos primeiro ver que componentes estão em rotação e a que distância estão do eixo de rotação. Bom, aqui temos a barra L 2 presa por uma das extremidades girando e a barra L 1 presa pelo centro, também em rotação. Como o eixo de rotação é perpendicular ao plano da página, ambas contribuições devem ser levadas em conta.

Outra coisa, as barras são homogêneas, isso quer dizer que M / L é contante.

Passo 2

Podemos colocar todas essas informações agora na integral do momento de inércia:

I = ∫ r 2 d m

Fazendo d m = M / L d r e assumindo que a distância r é ao longo das barras temos:

I = ∫ 0 L 2 M L 2   r 2 d r + 2 .   ∫ 0 L 1 / 2 M L 1   r 2 d r

Agora é só integrar! Vamos lá?

I = M L 2 . r 3 3 0 L 2 + 2 .   M L 1 . r 3 3 0 L 1 / 2

I = M L 2 2 3 + M L 1 2 12 = 0,2 . 0,5 2 3 + 2.0,2 0,4 2 12 = 0,02199 k g . m ²

Passo 3

Agora o problema coloca o eixo de rotação no centro da outra barra, na barra L 2 . A barra L 1 vai ser rotacionada por uma de suas extremidades e a barra L 2 , pelo seu centro.

Para facilitar nossa vida, podemos ir ali no passo anterior e pegar a integral já montada e só modificar os limites de integração =D

Agora a primeira integral vai de 0 até L 2 / 2   , multiplicado por dois, pois são duas metades de barra, e a segunda vai (multiplicado apenas por 1) de 0 até L 1 :

I = 2 . ∫ 0 L 2 / 2 M L 2   r 2 d r +   ∫ 0 L 1 M L 1   r 2 d r

Integrando obtemos esse resultado aqui ó (copiado do passo anterior, só mudei as letras!)

I = M L 1 2 3 + M L 2 2 12

Os valores de massa e comprimento das barras permanecem os mesmos, então é só jogar na calculadora:

I = 0,2 . 0,4 2 3 + 2.0,2 0,5 2 12 = 0,019 k g . m ²

Show!

Bora treinar mais?

Resposta

( a )   0,022 k g . m ²  

b 0,019 k g . m ²

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ato de equilibrar. Uma pequena esfera de massa M está ligada à extremidade de uma barra longa, fina e uniforme de comprimento L e massa M. a) Localize a posição do centro de massa do sistema barra-esf
Dois canos de 1,0m de comprimento, de mesma aparência, estão preenchidos com 10k g de chumbo, cada um. No primeiro cano, o chumbo está concentrado no meio, enquando no segundo cano o chumbo está divid
O momento de inercia de um corpo, em relação a um eico que não passa pelo seu centro de massa, é momento de inércia em relação a um eixo paralelo que passa pelo seu centro de massa: (a) sempre menor d
O disco B era idêntico ao disco A, até que um furo foi feito no centro do disco B. Qual dos dois discos tem o maior momento de inércia em relação ao eixo central de simetria? Explique sua resposta.
Considere o seu momento de inércia em relação a um eixo vertical que passa pelo centro do seu corpo, tanto quando você está de pé com seus braços junto ao corpo, quanto quando você está de pé com seus