Enunciado
Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 35.Exercício - Ex. 1
Duas fontes coerentes de ondas de rádio, e , estão a de distância uma da outra. Cada fonte emite ondas com comprimento de onda igual a . Considere pontos ao longo da linha reta entre as duas fontes. A que distância de , se houver alguma, a interferência é (a) construtiva e (b) destrutiva.
Passo 1
(a) O que vai definir se a interferência é construtiva ou destrutiva? A diferença de caminho!
No caso em que a interferência é construtiva, a diferença de caminho tem que ser um múltiplo inteiro do comprimento de onda:
No nosso caso, a distância entre as fontes é , e o comprimento de onda delas é .
Então a única forma de interferência construtiva é quando:
Nesse caso a interferência vai acontecer quando as ondas se encontrarem pela primeira vez, no meio do caminho entre e , ou seja, a de qualquer uma das fontes.
Passo 2
(b) Na interferência destrutiva, a diferença de caminho tem que encaixar nessa fórmula aqui:
Dessa vez, quando :
E quando :
Ou seja, só o caso “cabe” no intervalo de entre as duas fontes.
Passo 3
Vamos procurar os pontos em que essa diferença de caminho acontece:
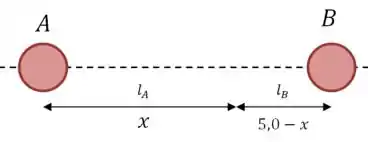
A gente quer achar os pontos em que a diferença dos caminhos é .
Então, começando com :
O caso simplesmente representa o caso em que e estão nas posições trocadas:
Ou seja, a interferência destrutiva pode ocorrer a ou a de uma das fontes.
Resposta
(a) A interferência construtiva ocorre a de uma das fontes.
(b) A interferência destrutiva ocorre a ou a de uma das fontes.