Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 35.Problemas Adicionais - Ex. 105
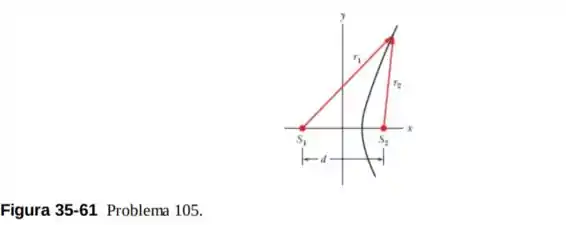
As duas fontes pontuais da Fig. 35-61 emitem ondas coerentes. Mostre que são hipérboles todas as curvas (como as que aparecem na figura) para as quais a diferença de fase entre os raios e é constante. (Sugestão: Uma diferença de fase constante significa uma diferença constante entre as distâncias e .)
Passo 1
Fala galerinha, beleza?
Esse exercício é um problema bem bonitinho em que vamos usar geometria analítica para resolver! A diferença de caminho ótico é
Para que a diferença de fase seja constante ao longo de uma curva, a diferença de caminho ótico deve ser constante. Por motivos que ficarão claros mais adiante, escreveremos a constante como sendo :
Se você souber que essa é a definição de uma hipérbole, o problema já está definido. Nos próximos passos vou partir dessa relação para chegar na equação da hipérbole do jeito que você deve conhecer!
Passo 2
Para adaptar a notação para geometria analítica, vamos escrever , de modo que
Assim, sendo , temos que
Logo,
Supondo , podemos tirar o módulo e escrever
Agora, elevamos ambos os lados ao quadrado:
Daí, abrimos os termos:
Simplificando por :
Passo 3
Elevamos novamente a equação ao quadrado:
Daí,
Estamos quase acabando. Vamos definir (é isso que fazemos na dedução da equação da hipérbole), de modo que
Dividindo a equação toda por :
Essa é a equação de uma hipérbole!
Resposta
Demonstação.