Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 5.6 - Ex. 5
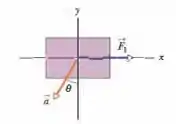
Duas forças agem sobre a caixa de vista de cima na Fig. 5-31, mas apenas uma é mostrada. Para , e , determine a segunda força (a) em termos dos vetores unitários e como um (b) módulo e (c) um ângulo em relação ao semieixo x positivo.
Passo 1
Então galera , neste problema, temos duas forças agindo sobre uma caixa e produzindo uma aceleração conhecida. Para determinar a força desconhecida, usamos a Segunda Lei de Newton. Vamos chamar as duas forças de e . De acordo com a Segunda Lei de Newton, , e , portanto, a segunda força é . Note que, como a aceleração está no terceiro quadrante, a força também deve estar no terceiro quadrante.
Na notação dos vetores unitários:
Assim, a segunda força é :
Passo 2
O módulo de nós sabemos que pode ser obtido através da relação:
Passo 3
Usando a trigonometria básica , sabemos que o ângulo que faz com o semieixo positivo pode ser determinado a partir da equação :
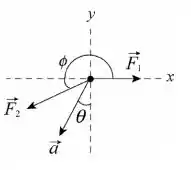
O ângulo pode ser ou . Como as componentes e são negativas, o ângulo correto é , que também pode ser expresso como . A figura abaixo mostra a solução. O resultado confirma nossa conclusão de que deveria estar no terceiro quadrante (o mesmo de ). A força resultante é :
que aponta na mesma direção de .
Tranquilo galera? Bora resolver mais exercícios então
Resposta
a)
b)
c)