Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Eletromagnetismo- Ed: 5º - Capítulo 19.Problemas - Ex. 72
Duas pequenas esferas de massa estão suspensas por cordas de comprimento que estão conectados em um ponto comum. Uma esfera tem carga e a outra, carga . As cordas fazem ângulos e com a vertical. (a) Explique como e estão relacionados. (b) Suponha que e sejam pequenos. Mostre que a distância aproximada entre as esferas é
Passo 1
Primeiro nós fazemos um desenho da situação desenhando as forças que agem em cada carga:
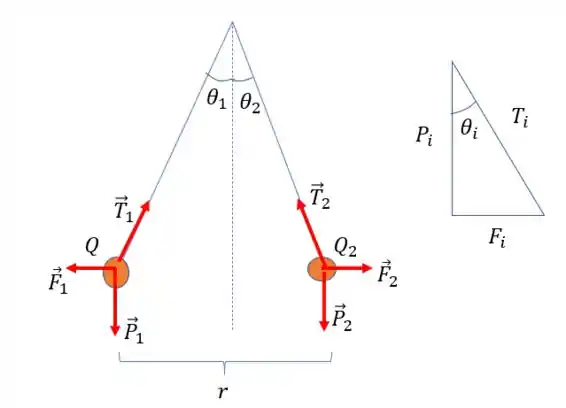
Observe que devemos desenhar a força peso, a tração do fio e a força de repulsão eletrostática. Note que eu desenhei um triângulo genérico que representa o equilíbrio de cada corpo. Para que as bolinhas fiquem em equilíbrio, devemos ter
Aqui vem o pulo do gato: sabemos que (mesma massa) e
Com isso, temos que
Logo, mesmo que as cargas de cada bolinha sejam diferentes, como elas possuem a mesma massa, os ângulos devem ser iguais:
Passo 2
Como os ângulos são iguais, vamos escrever . Vimos no passo 1 que
Substituindo e a expressão para discutida no passo 1, temos
Além disso, e , de modo que
Para ângulos pequenos, podemos usar a aproximação
Note que
Assim,
Portanto,
Logo,
Isolando , achamos