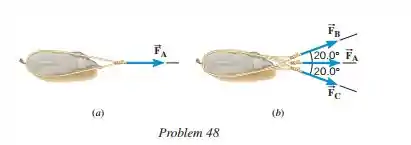
Um elefante bebê está preso em um buraco de lama. Para ajudar a retirá-lo, os tratadores usam uma corda para aplicar uma força , como mostra a parte a do desenho. Por si só, no entanto, a força é insuficiente. Portanto, dois adicionais forças e são aplicadas, como na parte do desenho. Cada um desses forças adicionais têm a mesma magnitude . A magnitude da força resultante atuando no elefante na parte do desenho é vezes maior do que na parte . Encontre a proporção quando .
Passo 1
Falaaaaaaaaaaaaaaaa Tribuxo?
Bora resolver mais uma questão!?
Vamos analisar as forças empregadas, como na parte só tivemos uma força aplicada, a resultante será a . Mas em , a gente já tem mais duas forças fora sendo aplicada, então teremos:
Como as duas novas forças aplicadas são idênticas:
Temos que a magnitude da força resultante é vezes maior que a magnitude de em , temos:
Passo 2
Agora para resolvermos o exercício precisamos encontrar uma expressão para em termos de e .
Vamos dizer que a direção é em e , e vamos considerar a resultante dos vetores que foram adicionados na parte , saca só o desenho:
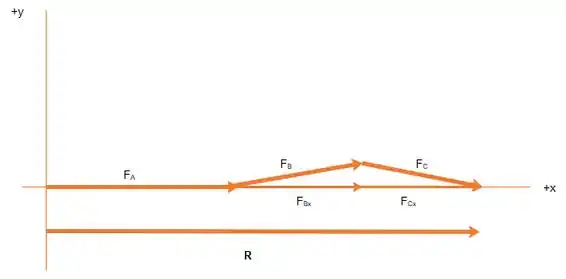
Como e são direcionados simetricamente em torno do eixo e têm a mesma magnitude , seus componentes y são iguais e opostos, então podemos cancelá-los na soma de vetores em , o nos deixa apenas com as componentes em de e . E temos também que tem apenas tem apenas componentes em , então podemos escrever:
E como todos estão na mesma direção, podemos escrever como:
Tá, mas como conseguimos os dados do e ???????
Lembra do macete de sempre, está deitado então está COm Sono:
Aplicando em :
Passo 3
Agora vamos lembrar, da fórmula:
Então, podemos aplicar quem é :
Podemos isolar :
Colocando em evidência:
Passo 4
Agora precisamos chegar na fração ...........
Para isso vamos começar dividindo tudo por :
Agora dividindo tudo por :
Temos que e , segundo o enunciado:
Foi divertido!!!!
Bora matar mais uma!