Qual a energia cinética máxima possível de um elétron envolvido no processo Compton em termos de energia do fóton incidente e da energia de repouso do elétron ?
Passo 1
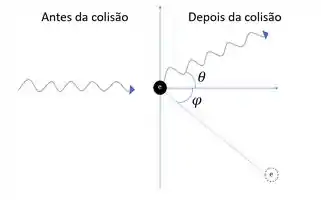
Assumindo uma colisão elástica, onde há conservação de energia temos:
A energia final do elétron é dada por:
Então temos:
Isolando o K, ficamos com:
Passo 2
A energia cinética não pode ser expressar em função da energia final do fóton, como é dito no enunciado do exercício, então, vamos escrever a em função da , com fizemos no exercício 17.
Conhecemos a relação entre e , dada pelo exemplo 2.4 do livro.
Então, temos a energia final do fóton:
O pode ser escrito em função da energia inicial do fóton, já que ele é o comprimento de onda do fóton incidente.
Substituindo na equação da :
Colocando o em evidência o denominador, resultamos na equação:
Somando as frações do denominador (dentro das regras matemáticas), temos:
Passo 3
Voltando para nossa equação da energia cinética:
Agora temos uma expressão, como termos aceitáveis pela questão, para substituir na equação da energia cinética.
Resposta
Mesmo com uma expressão pouco amigável, conseguimos fazer uma boa análise. A questão pede a máxima energia cinética, quer dizer, o maior valor possível que a energia cinética pode assumir. Para isso, a parcela correspondente a energia final do fóton tem que ser a menor possível, pois dessa forma, vai “retirar” da o menor valor, e isso vai ter como resultado um maior K.
Para que a expressão abaixo seja a menor possível…
O denominador tem que ser o maior valor. Para exemplificar melhor, vou usar uma analogia:
Percebe que quanto maior for o denominador, menor será o resultado da divisão? O que estamos procurando para o nosso exemplo, é a mesma coisa, qual é o maior valor que o denominador pode assumir. Sabemos que são constantes. O único componente que pode variar é o , então o maior valor que pode assumir, é 2, para quando o ou qualquer múltiplo ímpar de .
Então a maior energia cinética possível é dada por: