Uma esfera de de diâmetro e massa de encontrase em equilíbrio hidrostático imersa em um líquido. Identifique o líquido.
Passo 1
Bom, galera, aqui a gente vai precisar montar a equação que rege todas as forças que agem sobre a esfera.
Por isso, vamos fazer um diagrama de corpo livre pra ela...
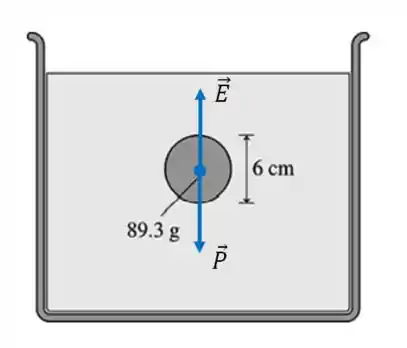
As forças no caso aí são: o peso e o empuxo
Primeiro temos que apontar as forças. O empuxo aponta pra cima, enquanto o peso pra baixo.
Como o bloco está em equilíbrio, a soma das forças dará zero:
Vamos calcular essas duas forças!
O peso é dado por:
Onde !
Passo 2
O Empuxo é dado por:
Mas não sabemos . No entanto, temos como obter o volume de líquido deslocado , uma vez que a esfera está completamente imersa no líquido e sabemos seu raio.
Ora bolas! é o próprio volume da esfera...
Dessa forma, isolando ao igualar com :
E substituindo os valores numéricos...
Dando uma olhada na tabela 15.1:
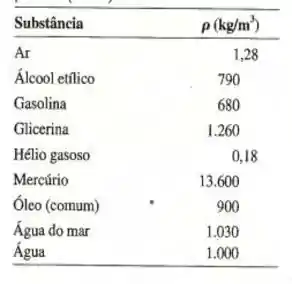
Podemos ver que o líquido, cuja densidade mais se adequa ao resultado obtido é o álcool etílico!