Um espelho esférico de raio R tem centro em C, como mostrado na FIGURA P23.78. Um raio paralelo ao eixo é refletido através de F, o ponto focal. Mostre que se . 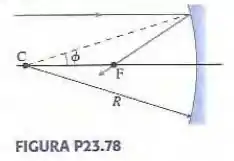
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!!
Primeiro nós vamos nos concentrar no eixo óptico e no raio paralelo a ele. A geometria diz se linhas paralelas são ambos cortados por uma diagonal (neste caso, a linha que passa pelo centro de curvatura e normal ao espelho no ponto de incidência) os ângulos internos são iguais; então . A lei da reflexão diz que , então nós concluímos que . Agora concentre-se no triângulo cujos lados são R, a e b. Porque dois dos ângulos são iguais, então é um triângulo isósceles, portanto, . Aplica a lei dos cossenos a este triângulo, tal como
Como , nós temos que
Temos que o termo R, é igual a
Nós queremos a magnitude do termo a nos termos de R, para isso, precisamos primeiro resolver para a
Se então , então vamos pensar, se o limite for um pequeno ângulo , então , então desde que , também deve ser dessa forma
Demonstrando o que a questão nos pede 😊.
Resposta
Ei, a resposta está no passo a passo :)