Enunciado
Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 34.Exercícios e Problemas - Ex. 82
Uma espira quadrada e fechada é formada com 40 cm de fio, tendo , como mostrado na FIGURA PD34.84. Um campo magnético de é perpendicular à espira. Em, dois vértices diagonais opostos da espira começam a se afastar um do outro a .
- Em quanto tempo a espira colapsará, transformando-se em uma linha reta?
- Obtenha uma expressão para a corrente induzida I, em função do tempo, enquanto a espira está colapsando. Considere que os lados permaneçam retos durante o colapso.
- Calcule I para quatro ou cinco instantes de tempo durante o colapso e, então, desenhe o correspondente gráfico I versus t.
Passo 1
Faaaaaala, galera... Tranquileba??
Paraa )
Sabemos que conforme cada lado vai se separando, a espira quadrada vai se esticando até se tornar uma reta, e podemos visualizar a o seu estiramento com a sua altura dessa forma: (sendo b o lado da espira)
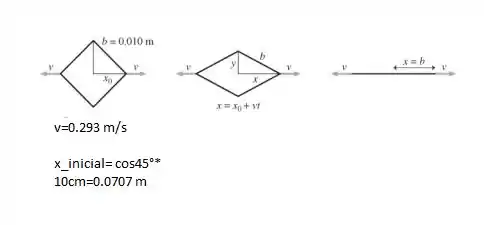
E temos que:
Pede- se quando a espira se torna uma reta, ou seja, de altura de 0, logo:
Quando se tornar uma reta:
Mas temos que:
Assim:
Aplicando valores:
Bora pro próximo passo?!
Passo 2
Para b)
Tomemos e por definição:
E nesse caso sendo constante:
E enquanto colapsa a a rea total é quadrado vezes a área da área que temos antes:
De forma que a área total é:
E dado antes o valor de y:
Ou seja. Area varia!
Assim, voltando a:
Vamos abusar um pouco da bondade matemática e fazer:
Assim:
E derivemos aplicando a regar da cadeia
Temos os valores de tudo no passo 1,logo substituindo-os:
Pede-se a corrente e sabemos por definição:
Logo:
Eita que conta feia né? lsksks
Passo 3
Para c)
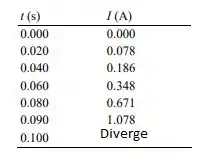
Aplicando os tempos de es
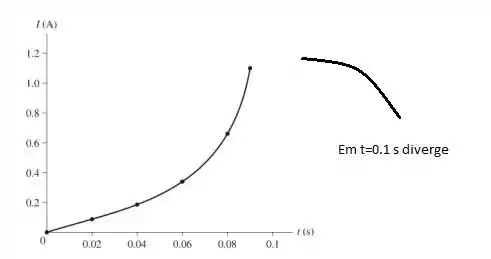
Veja que em diverge, pois o denominador vai pra 0
Temos:
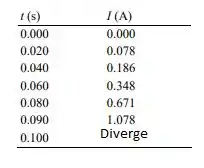
E o gráfico é:
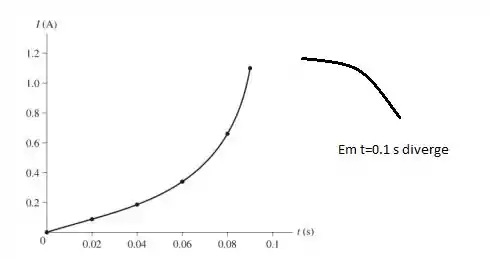
Resposta
Para a)
Para b)
Para c)
