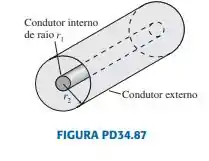
Sinais de alta freqüência são geralmente transmitidos ao longo de um cabo coaxial, tal como o mostrado na FIGURA PD34.87. Por exemplo, o cabo de conexão de sua TV por assinatura é desse tipo. O sinal é transportado pelo fio de raio , enquanto o condutor externo, de raio , está aterrado. Um material isolante, leve e flexível preenche o espaço entre eles, e um isolante plástico cobre a combinação pelo lado de fora.

1. Encontre uma expressão para a indutância por metro de um cabo coaxial. Para tal, considere o fluxo através de um retângulo de comprimento l que se estenda através do intervalo entre o condutor interno e o externo.
2. Calcule a indutância por metro de um cabo coaxial com e

Dado que “considere o fluxo através de um retângulo de comprimento l que se estenda através do intervalo entre o condutor interno e o externo.”, então E o campo elétrico dentro de um fio longo é dapor pela lei de gauss para o fluxo magnético, isto é:

Sendo um fio longo:

Assim:

Do raio interno ao externo:

Assim a indutância é:

Mas pede- de a indutância por metro de um cabo coaxil, logo:

Para b)

Aplicando valores na equação que achamos no item a)

Concluímos que: