Enunciado
Física - Young and Freedman - Vol 3- Ed: 14º - Capítulo 29.Exercícios - Ex. 46
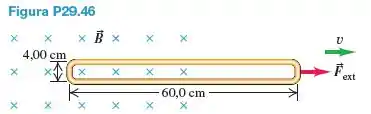
Uma espira retangular muito longa pode deslizar sem atrito sobre uma superfície horizontal. Inicialmente, a espira possui parte de sua área em uma região de campo magnético uniforme, com módulo , perpendicular ao plano da espira. A espira possui dimensões de por , massa de e resistência . A espira encontra-se inicialmente em repouso; depois, uma força constante é aplicada à espira para puxá-la para fora do campo (Figura P29.46).
(a) Qual é a aceleração da espira quando ?
(b) Quais são a velocidade terminal da espira e sua aceleração quando ela está se movendo nessa velocidade terminal?
(c) Qual é a aceleração da espira quando ela está completamente fora do campo magnético?
Passo 1
Olá, tudo bem? Vou ajudar você aqui!
Letra (a):
Da segunda lei de newton temos:
E a força induzida é:
E a aceleração é:
Passo 2
Letra (b):
A velocidade terminal é quando a força resultante é nula. Então da expressão para a segunda lei de Newton do passo anteiro temos:
Passo 3
Letra (c):
E usando a segunda lei novamente temos:
Espero ter ajudado! =D