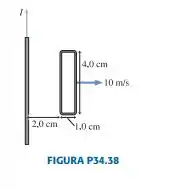
A espira retangular mostrada na FIGURA P34.38 tem resistência de . Qual é a corrente induzida na espira neste instante?
Passo 1
Faaaaaala, galera... Tranquileba??
Antes, precisamos saber a relação da fem com o fluxo magnético criado pelo campo magnético de um fio que conduz corrente próximo de uma espira. Bora lá?!
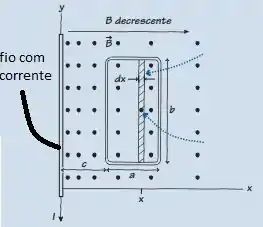
Assim:
Sendo para um fio que conduz corrente a uma distancia x do fio:
Assim:
Sabemos por definição que:
Bora pro próximo item?!
Passo 2
Agora o que vamos fazer os matemáticos odeiam ksksk vamos multiplicar e dividir por dx, assim:
Sabemos que
Veja antes de tudo que a corrente desta equação é a qual passa no fio, não na espira como foi pedido
Passo 3
Pede-se a corrente na espira, logo:
Colocando valores:
Concluímos que:
Onde depende da corrente do fio.