Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 34.Exercícios e Problemas - Ex. 28

Temos uma bobina com 5,0   c m de diâmetro, 20 espiras e resistência total de 0,50   Ω , e um campo magnético perpendicular à bobina com módulo B =   0,020 t + 0,010   t 2 , onde B está em tesla, e t, em segundos.

  1. Desenhe o gráfico de B em função do tempo desde t =   0   s até t = 10   s .
  2. Obtenha uma expressão para a corrente induzida I(t) em função do tempo.
  3. Calcule I em t =   5   s e t = 10   s .

Passo 1

Faaaaaala, galera... Tranquileba??

Para a)

Fazendo um gráfico de B ( t ) temos:

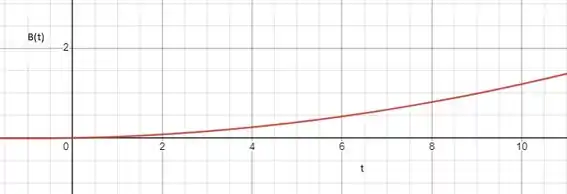
Bora pro próximoitem?!

Passo 2

Para b)

Aqui já é mais conceitual. Sabemos que:

ε = d ϕ b d t

E:

ϕ b = ∮ S B → ∙ n v e r s o r d A →

Sendo B constante e perpendicular a bobina:

ϕ b = B * A

E sendo uma bonina de N espiras:

ϕ b = B * A * N

Assim:

ε = A * N d d t 0,020 t + 0,010   t 2

ε = A * N 0,020 + 0,02 0   t

Aplicando valores:

ε =   π 1 2 5 × 10 - 2   m 2 20 ( ( 0.020 t + 1   T s = 7.9 × 10 - 4   1 + t   V

Sabemos que:

ε t = R * i t → i t = ε t R

Aplicando valores:

i t = 7.9 × 10 - 4   1 + t   V 0.50   Ω = 1.6 × 10 - 3   ( 1 + t )   A

Passo 3

Para c)

Para t = 5   s :

i t = 5 = 1.6 × 10 - 3   1 + 5 A = 9.6 × 10 - 3   A

Para t = 10   s :

i t = 10 = 1.6 × 10 - 3   1 + 10 A = 1.7 × 10 - 2   A

Resposta

Para a)

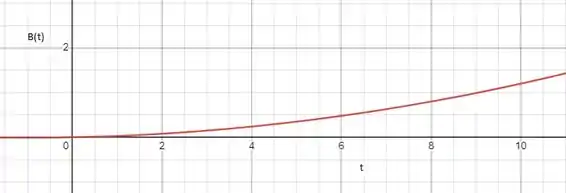
Para b)

i t = 1.6 × 10 - 3   ( 1 + t )   A

Para c)

Para t = 5   s :

i t = 5 = 9.6 × 10 - 3   A

Para t = 10   s :

i t = 10 = 1.7 × 10 - 2   A

Ver Outros Exercícios desse livro