Estenda o resultado do problema anterior ao caso ele um corpo rígido, para obter
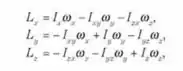
em que
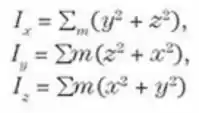
são os momentos de inércia relativos aos três eixos coordenados, de acordo com a Eq. (10.7), e
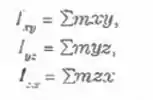
são chamados os produtos de inércia. Comparando estes resultados com a Eq. (10.5), você poderá reconhecer que os eixos principais são aqueles para os quais os três produtos de inércia são nulos. Note também que o comportamento de um corpo rígido quanto às rotações é determinado em geral por seis quantidades: os três momentos de inércia e os três produtos de inércia.
Passo 1
E aiii galerinha!! Aqui, teremos que lembrar da seguinte fórmula:
Assim, teremos que:
Passo 2
A partir disso, conseguimos provar que
E, da mesma forma, para as outras componentes em y e z.
Resposta
Ei, a resposta está no passo a passo :)