Faça um gráfico das energias cinética e potencial como função de (a) tempo e (b) altura, para um corpo que cai de uma altura h, estando inicialmente em repouso. Verifique que as curvas, em cada caso, dão uma mesma soma constante.

Já a energia potencial, será em função da altura h que o corpo cai. Desta forma, teremos:

Logo, temos que:

Agora, vamos pensar um pouco na prática deste caso. Nós temos um corpo caindo, do repouso, atingindo o solo. Após sair do repouso, o corpo terá energia cinética cada vez maior, até que seu movimento seja cessado, e a energia passe a cair novamente, certo?

Ok, além disso, precisamos entender que a energia potencial gravitacional estará agindo sobre o corpo até que a altura do mesmo seja igual a 0. Assim, a energia gravitacional diminui à medida que a altura do corpo em relação ao solo diminui, ou seja, à medida que o tempo aumenta. A partir disso, concordam comigo que, em função do tempo, teremos uma curva de crescimento, que, de ambas as energias será inversa? E que, em função da altura, teremos retas (já que altura tem relação linear com as energias) que também serão inversas? Ou seja, em relação ao tempo, à medida que a energia cinética aumenta, a energia gravitacional diminui e, em relação à altura, o gráfico é linear?

Certo, vamos desenhar isso nos gráficos agora:

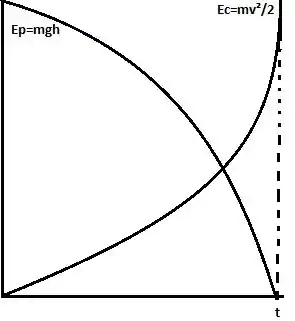
e:

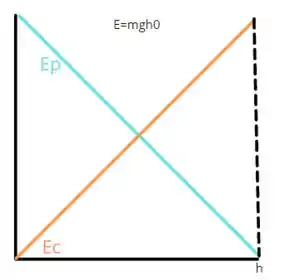
Pronto! Esse é o gráfico da energia cinética e da energia potencial gravitacional em função do tempo e em função da altura!