Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 36.Problemas adicionais - Ex. 109
Quando fazemos na Fig. 36-50, as duas fendas se tornam uma única fenda de largura . Mostre que, nesse caso, a Eq. 36-19 e a Eq. 36-5 levam ao mesmo resultado
Passo 1
E aí meus caros(as)! A questão da vez agora é a 106!
Bom! Temos aqui uma questão sobre difração em fendas!
E o objetivo é mostrar que as seguintes equações, quando , levam ao mesmo resultado...
Passo 2
Pois muito bem! Vamos considerar as duas equações abaixo...
supondo ângulos iguais
Supondo ângulo iguais e comprimento de ondas iguais, podemos estabelecer a seguinte relação...
Só que a distância é medida do centro de uma fenda ao centro da outra fenda, o que, em nosso caso, significa que . Assim...
Passo 3
Vamos agora interpretar esse resultado!
Em primeiro lugar, a divisão não é válida para (que corresponde a ), de modo
que nosso raciocínio não se aplica ao máximo central.
Em segundo lugar, a equação abaixo fornece a posição das franjas de interferência claras ...
Enquanto a equação abaixo fornece a posição das franjas de difração escuras...
Quando as posições coincidem, a franja é escura, como mostra a figura abaixo...
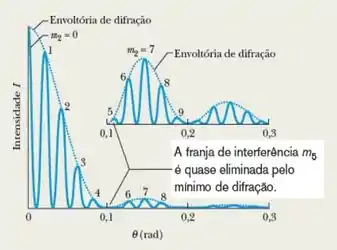
Para , a relação , significa que é um número par. Logo, as Eq. 36-19 e a Eq. 36-5 levam ao mesmo resultado.
Resposta
Costumamos chamar informalmente de “azul” o comprimento de onda de 400 nm e de “vermelho” o comprimento de onda
Costumamos chamar informalmente de “azul” o comprimento de onda de 400 nm e de “vermelho” o comprimento de onda
em que q é a posição angular da linha associada ao comprime