Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 36.Problemas adicionais - Ex. 104
Um feixe de raios com comprimentos de onda entre e é espalhado por uma família de planos de um cristal. A distância interplanar é . Observa-se que são produzidos feixes difratados para comprimentos de onda de e . Qual é o ângulo entre o feixe incidente e o feixe espalhado?
Passo 1
E aí meus caros(as)! A moda agora é a questão 101!
Bom! Temos aqui uma questão sobre difração de raios !
E o nosso objetivo aqui é obter aqui, o ângulo entre o feixe incidente e o feixe espalhado!
Não seja por isso! Pra difração de raios , temos a seguinte equação abaixo...
E a gente tem aqui dois comprimentos de onda pra analisar! Um de e . Vamos chamar o espalhamento pertinente a de e o espalhamento de de .
Desse modo, como temos a mesma distância interplanar para ambos os casos, ficamos com...
Passo 2
Agora, é uma questão de ver quais valores de e satisfazem a relação anterior!
É só testar valores! Um par perfeito que iria satisfazer a igualdade anterior é...
e
Conforme podemos ver logo abaixo...
Passo 3
Dessa forma, voltando àquela primeira equação do ...
Isolando :
Uma vez que e usando ...
E pra descobrir o ângulo entre o feixe incidente e o feixe espalhado, vamos dar uma olhada na figura abaixo...
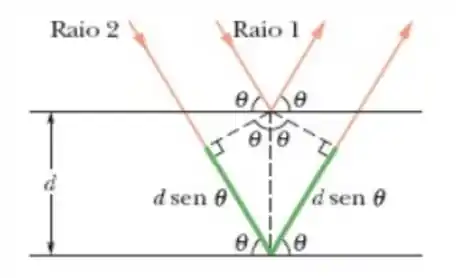
Conforme podemos ver, o ângulo que nós queremos obter é dado por...
E como ...
em que q é a posição angular da linha associada ao comprimen