A partir da (2.20), trace um gráfico de () em função de (), tomando para () os pontos , , , e . Para cada um desses pontos calcule o aumento lateral. Interprete os resultados em termos de objetos reais ou virtuais, imagens reais/virtuais, eretas ou invertidas, para com uma dos pontos acima, fazendo o traçado de raios correspondentes, (a) para um espelho côncavo; (b) para um espelho convexo.
Passo 1
A equação que relaciona , e é:
Portanto,
Logo,
Vamos chamar
Assim,
Logo,
Queremos fazer o gráfico de como função de .
Passo 2
Podemos escrever ainda:
Vamos impor que para que o objeto esteja sempre na frente do espelho (seja real). Nos casos que , temos que (espelho côncavo). Portanto, para o item (a), temos o seguinte gráfico
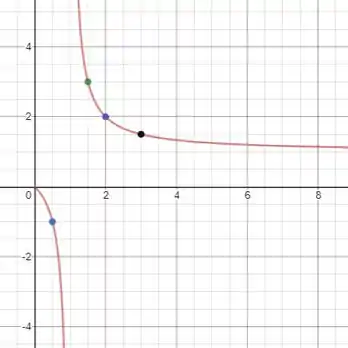
Marquei os pontos com , , e . O ponto com não foi marcado pois a função diverge nesse ponto.
O aumento lateral é dado por
Considerando os casos com (espelho côncavo), obtemos os resultados da tabela:
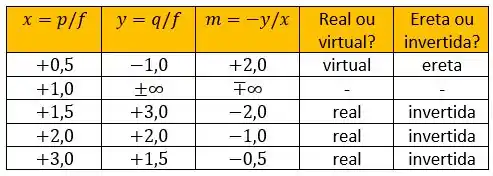
Na interpretação da tabela, vemos que para , isto é, , não há formação de imagem. Portanto, não há formação de imagem quando o objeto é posicionado sobre o foco do espelho côncavo.
Além disso, como , o sinal de é o sinal de . Portanto, , que implica imagem real. Analogamente, implica imagem virtual. Por fim, o sinal de determina se a imagem é ereta ou invertida: imagem ereta e imagem invertida.
Passo 3
Agora vamos seguir olhando para objetos reais (), mas com (espelho convexo). Este é o item (b)!
Nesse caso, vamos pegar os pontos , , , e :
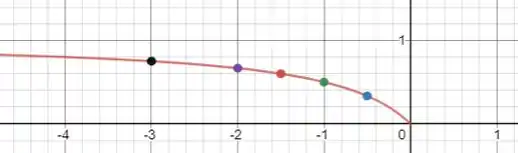
Nesse caso, em todos os pontos temos formação de imagem! Em todas elas . Como , temos que . Com isso, vemos que todas as imagens são virtuais, formadas atrás do espelho!
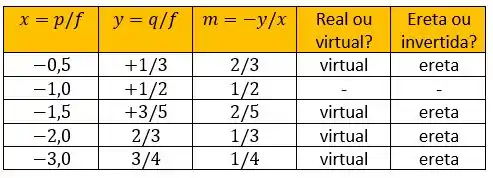
Resposta
Gráfico.