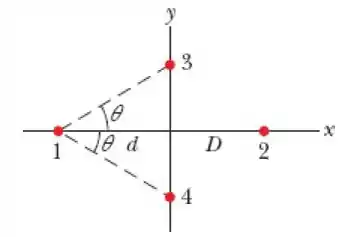
A Fig. 21-31 mostra um sistema de quatro partículas carregadas,com e . A carga da partícula 2 é ; a carga das partículas e é . (a) Qual deve ser a distância entre a origem e a partícula para que a força que age sobre a partícula seja nula? (b) Se as partículas e são aproximadas do eixo mantendo-se simétricas em relação a esse eixo, o valor da distância é maior, menor ou igual ao do item (a)?
Passo 1
Faaaaaaalaaa galerinha, animados para continuar?
Então booora!!
Antes de qualquer coisa nós vamos mostrar este desenho com as forças eletrostática atuando lá na nossa carga 1, tudo bem?
Nós também já sabemos que a distância de 1 até a origem vale e que a distância de 2 até a origem , para facilitar nossa vida futura vou chamar a distância de 1 até 3 e 4 por e , tranquilinho né?
Vamos ver?
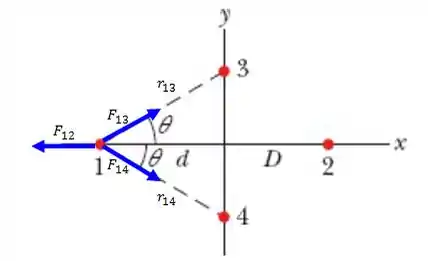
A trigonometria nos diz que:
Sendo assim:
Sabemos que:
Então:
Belezaa !! Agora vamos guardar esta informação no nosso coração !!
Passo 2
Agora que sabemos todas as distâncias entre as cargas, o que fazemos?
Lembramos da Lei de Coulomb, certo?
Onde e são as cargas, a distância e é a constante elétrica que vale
Agora vamos calcular as forças eletrostáticas que atuam na carga 1?
O problema nos disse que a força resultante que age sobre a partícula é nula na direção x, ok?
Substituindo as forças na direção usando a trigonometria:
Substituindo:
Vamos colocar nossos dados?
Vamos tirar a raiz dos dois lados, ok?
Finalizamos a letra (a), mas ainda tem a (b) !!
Passo 3
Bom galerinha, na letra (b) nós temos uma teoria bem legal !!
Quando as cargas 3 e 4 se aproximam do eixo x o ângulo diminui, e o que acontece com o cosseno ?
Aumenta, né? Se o cosseno aumenta, as componentes das forças na direção x, e também aumentam, certo?
Para compensar este aumento nas forças eletrostáticas de 3 e 4, a força eletrostática de 2 também deve aumentar para manter a força resultante nula!!
Se lembrarmos da Lei de Coulomb, para aumentar a força eletrostática nós devemos diminuir a distância entre elas, certo?
Então a distância deve diminuir !! Ou seja, o valor de deve ser menor do que o valor que encontramos na letra (a)!!
Gostaram ?!
Resposta
- Menor.