Na Fig. 21-31, as partículas e , de carga , estão no eixo , a uma distância da origem. A partícula , de carga , é deslocada ao longo do eixo , de até . Para que valor de o módulo
da força eletrostática exercida pelas partículas e sobre a partícula é (a) mínimo e (b) máximo? Qual é o valor (c) mínimo e (d) máximo do módulo?
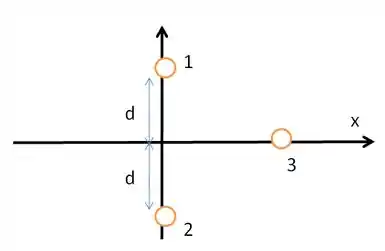
Passo 1
Shoow galerinha, mais uma bem parecida com a anterior, ok?
Vamos colocar no desenho?

A trigonometria nos diz que:
Nós podemos tirar mais uma informação importante aqui para usarmos la na frente, o cosseno!!
O problema não nos deu o ângulo, mas a trigonometria nos diz que:
Belezaa !! Agora vamos guardar esta informação no nosso coração !!
Passo 2
Agora que sabemos todas as distâncias entre as cargas, o que fazemos?
Lembramos da Lei de Coulomb, certo?
Onde e são as cargas, a distância e é a constante elétrica que vale
Agora vamos calcular as forças eletrostáticas que atuam na carga 3?
Como a força está sendo aplicada na carga 3 de forma angular, teremos uma componente dela na direção x e outra na y, certo?
Como as cargas 1 e 2 são as mesmas, assim como o ângulo que els fazem com o eixo x, as componentens na direção y se anulam, não é?
Então vamos olhar as forças em x:
Lembrando mais uma vez da trigonometria:
Vamos substituir as forças e o cosseno ?
Sabemos que:
Então:
O problema nos disse mais uma coisa muito importante, que vai de até , portanto a força mínima é obtida quando !
E a força máxima?
Simples !! Basta nós derivarmos e igualarmos a zero:
Isolando x:
Substituindo :
Ihuuuul !! Já achamos (a) e (b), mas ainda precisamos de achar (c) e (d) !!
Passo 3
Nas letra (c) e (d) precisamos achar o valor da força, ok?
No primeiro caso temos
Molezinha, né?
Agora quando
E chegamos ao fim de mais uma !!