Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 22.Problemas Adicionais - Ex. 82

Na Fig. 22-61, a partícula 1 (de carga +2,00 pC), a partícula 2 ( de carga - 2,00 pC) e a partícula 3 ( de carga + 5,00 pC) formam um triângulo equilátero de lado a = 9,50 cm. (a) Determine a orientação (em relação ao semieixo x positivo) da força F3 a que a partícula 3 é submetida pelas outras partículas fazendo um esboço das linhas de força associadas às outras partículas. (b) Calcule o módulo da força F3

Passo 1

Então, temos três partículas carregadas, onde a partícula 1 tem carga q1 = +2,00 pC, a partícula 2 tem carga q2=-2,00 pC e a partícula 3 tem carga q3= +5,00pC. Essas partículas formam um triângulo equilátero de lado a= 9,50 cm.

Para responder o item (a), vamos pensar na soma vetorial da força que a partícula

1 faz na 3, F13, e na força que a partícula 2 faz na 3, F23. Sabemos que seus módulos vão ser iguais, porém com direção opostas, por causa do sinal das cargas. Dessa forma, a soma delas deve anular as componentes na direção y, fazendo com que F3 só tenha direção no eixo x. Fica mais fácil desenhando:

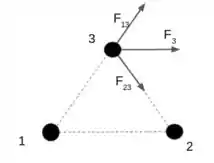
Passo 2

Para o item (b), podemos usar a relação entre duas retas paralelas, para descobrir que o ângulo, θ, que F23 e F13 fazem com o eixo x é θ= 60º. Portanto, para acha a relação entre os vetores basta somar o módulo da componente horizontal deles:

Como, o módulo dos vetores é igual:

Podemos utilizar a lei de Coulomb:

Resposta

(a) O vetor tem componente apenas na direção x

(b)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Três longas linhas de carga, de sinais iguais, módulos iguais e densidades lineares de carga iguais, estão dispostas perpendicularmente ao plano de página, como mostra a Fig.24-23. Esboce as linhas de

Esboce qualitativamente as linhas de campo elétrica entre duas cargas esféricas concêntricas e condutoras e também fora delas, sabendo que a casca interna tem uma carga positiva q 1 e a casca externa

Uma partícula α , núcleo de um átomo de hélio, tem uma massa de 6,64 ∙ 10 27 K g e uma carga de + 2 e . Quais são o módulo, a direção e sentido do campo elétrico que equilibraria seu peso?

Um objeto tendo uma massa de 10,0g e uma carga de + 8,00 × 10 - 5 C é colocado num campo elétrico E → com E x = 3,00 × 10 3 N / C , E y = - 600 N / C e E z = 0 . (a) Quais são o módulo, a direção e o

Em uma de suas experiencias, Milikan observou para a carga de uma mesma gota em instantes diferentes, os seguintes valores.Que valor para a carga elementar e pode ser deduzido desses dados?