Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 9ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 9º - Capítulo 25.Problemas Adicionais - Ex. 61
A Fig. 25-54 mostra o capacitor 1 () , o capacitor 2 () e o capacitor 3 () ligados a uma bateria de 12,0 V. Quando a chave Sé fechada, ligando ao circuito o capacitar 4 (), inicialmente descarregado, determine (a) o valor da carga que passa pelo ponto P, proveniente da bateria; (b) o valor da carga armazenada no capacitar 4. (c) Explique por que os resultados dos itens (a) e (b) não são iguais.
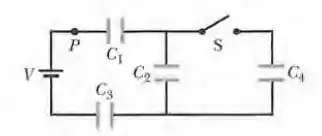
Passo 1
Aqui temos um circuito que já está com os capacitores carregados e se liga a um quarto capacitor descarregado, teremos que calcular a carga que passa pelo pornto P, o valor da carga armazenada em 4 e porque os itens (a )e (b) não são iguais, portanto vamos começar pela primeira situação onde os capacitores estão ligados em série e podem ser substituídos por um capacitor equivalente, que vamos chamar de . Resolvendo a equação
obtemos . Como , a carga do circuito é
Na situação final, e estão em paralelo e podem ser substituídos por uma capacitância equivalente a , que está em série com e . A capacitância equivalente do circuito é obtida resolvendo a equação
que nos dá. Assim, a carga final é
Passo 2
(a) A carga que passa pelo ponto P é a diferença entre a carga final e a carga inicial:
Passo 3
(b) O capacitor , que usamos para substituir e , está em série com e e, portanto, também adquire uma carga . Assim, a tensão entre os terminais de é
Como esta tensão é a mesma que existe entre os terminais de e de , o que nos dá
Passo 4
(c) A bateria fornece carga apenas às placas às quais está ligada; a carga das outras placas
se deve apenas à transferência de elétrons de uma placa para outra, de acordo com a nova
distribuição de tensões pelos capacitores. Assim, a bateria não fornece carga diretamente ao
capacitor.
Resposta
(a)
(b)