Exercícios de Campo e Energia em um Capacitor. - Lista de Exercícios Resolvida

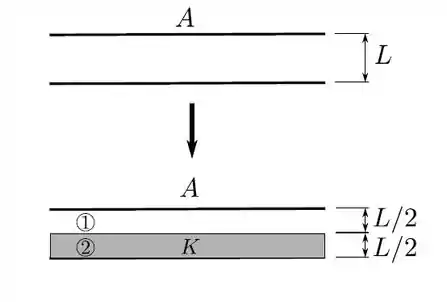
Um capacitor plano-paralelo tem placas idênticas de área , cada uma, com separação entre elas (conforme parte superior da figura ao lado). Numa primeira etapa, tal capacitor é ligado a uma bateria até atingir um módulo de diferença de potencial entre suas placas e, imediatamente, desconectado da bateria.

1. Determine o módulo do campo elétrico e a energia eletrostática armazenada

Numa segunda etapa um isolante de constante dielétrica é inserido no capacitor, preenchendo pela metade região entre suas placas, conforme mostrado na parte inferior da figura ao lado.

2. Determine o módulo da nova diferença de potencial entre as placas.
3. Determine o módulo (, , ) do novo campo elétrico em cada uma das duas “metades” ( e ) entre as placas.
4. Determine a nova energia eletrostática armazenada .

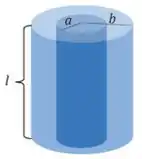
Seja o capacitor cilíndrico da figura abaixo, com a placa interna carregada com carga negativa , de tal forma que a placa externa tenha a mesma carga, em módulo, porém positiva.

(a) Determine a densidade de energia entre suas placas.

(b) Determine a energia armazenada neste capacitor, usando a relação , onde é um elemento de volume.

A diferença de potencial entre as placas de um capacitor de é de .

a) Quanta energia é armazenada no capacitor?

b) Quanta energia adicional é necessária para aumentar a diferença de potencial entre as placas de para ?

Para a segurança dos clientes, o supermercado utiliza lâmpadas de emergência e rádios transmissores que trabalham com corrente contínua. Para carregar suas baterias, no entanto, esses dispositivos utilizam corrente alternada. Isso é possível graças a seus retificadores que possuem, cada um, dois capacitores de , associados em paralelo. Os capacitores, descarregados e ligados a uma rede elétrica de tensão máxima igual a 170 V, estarão com carga plena após um certo intervalo de tempo t. Considerando t, determine:

a) a carga elétrica total acumulada;

b) a energia potencial total armazenada.

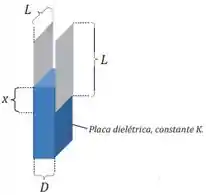
Duas placas condutoras quadradas, cada qual com lado igual a , são separadas por uma distância . Uma placa dielétrica com constante dielétrica e com dimensões é inserida até uma distância no espaço entre as placas, como indica a figura.

(a) Calcule a capacitância do sistema.

(b) Suponha que o capacitor seja conectado a uma bateria que mantém uma diferença de potencial constante entre as placas. Se a placa dielétrica for inserida até uma distância adicional no espaço entre as placas, mostre que a variação de energia acumulada é dada por:

(c) Suponha que, antes de a placa se mover uma distância , as placas sejam desconectadas da bateria, de modo que as cargas das placas permaneçam constantes. Determine o módulo da carga em cada placa e a seguir mostre que, quando a placa penetra mais uma distância no interior do espaço entre as placas, a energia acumulada varia de uma quantidade igual em módulo, mas de sinal contrário ao valor encontrado no item (b).

Um capacitor possui placas paralelas separadas por uma distância igual a . O espaço entre as placas está cheio de poliéster (Constante dielétrica, ), que possui rigidez dielétrica . Qual a voltagem máxima, e a carga máxima possível que o capacitor pode suportar sem que ocorra ruptura dielétrica.

Considere que na ausência do poliéster o capacitor possui capacitância .

;

;

;

;

;

Qual das seguintes afirmativas é falsa?

1. No processo de carregamento de um capacitor, cria-se um campo elétrico entre suas placas.
2. O trabalho necessário para se carregar um capacitor pode ser pensado como o trabalho necessário para se criar um campo elétrico entre suas placas
3. A densidade de energia na região entre as placas de um capacitor depende linearmente do módulo do campo elétrico
4. A diferença de potencial entre as placas de um capacitor plano paralelo depende linearmente do módulo do campo elétrico
5. Ao dobrarmos a carga em cada uma das placas de um capacitor dado, dobramos a diferença de potencial entre suas placas

Um capacitor de é usado em uma câmera fotográfica para armazenar energia. Suponha que o capacitor foi carregado a . Qual é o valor da energia armazenada?

Considere as três seguintes afirmações:

A densidade de energia em um campo elétrico é linearmente proporcional ao módulo de tal campo.

O trabalho necessário para carregar um capacitor pode ser pensado com o trabalho necessário para criar um campo elétrico.

Para um dado capacitor, quando dobramos a carga em cada uma de suas placas, a capacitância também dobra.

Qual alternativa indica a(s) afirmação(ões) correta(s)?

Somente a .

Somente a .

Somente a .

Somente a e a .

Somente a e a .

Somente a e a .

Todas estão corretas.

Nenhuma está correta.

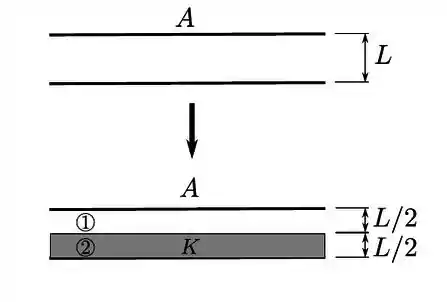
Um capacitor plano-paralelo tem placas idênticas de área , cada uma, com separação entre elas (conforme parte superior da figura ao lado). Numa primeira etapa, tal capacitor é ligado a uma bateria até atingir um módulo de diferença de potencial entre suas placas e, imediatamente, desconectado da bateria.

1. Determine o módulo do campo elétrico e a energia eletrostática armazenada

Numa segunda etapa um isolante de constante dielétrica é inserido no capacitor, preenchendo pela metade região entre suas placas, conforme mostrado na parte inferior da figura ao lado.

2. Determine o módulo da nova diferença de potencial entre as placas.
3. Determine o módulo (, , ) do novo campo elétrico em cada uma das duas “metades” ( e ) entre as placas.
4. Determine a nova energia eletrostática armazenada .

Considere um capacitor esférico formado por um condutor interno de raio e um condutor externo de raio , conforme a figura. O espaço entre os condutores é preenchido com material de constante dielétrica .

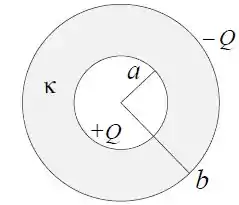
Carrega-se o condutor interno com carga e o externo com carga (cargas livres). O campo elétrico devido apenas a essas cargas livres é

Onde é a distância ao centro do capacitor esférico.

Escreva a expressão do vetor campo elétrico dentro do dielétrico .

Calcule a energia armazenada no capacitor na ausência de dielétrico (em função de , e ), e a energia na presença do dielétrico (em função de e ).

Calcule o vetor campo elétrico devido somente às cargas induzidas (ligadas) no dielétrico.

Considere um capacitor de placas planas, paralelas, com área , separadas por uma distância no vácuo.

Calcule a capacitância deste capacitor no vácuo em função de ,

e .

Calcule a nova capacitância do capacitor se preenchermos parcialmente o espaço entre as placas com um material de constante dielétrica e espessura , conforme a figura. Forneça sua resposta em função de e .

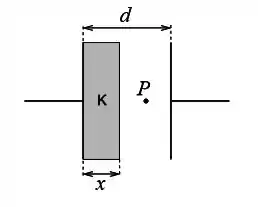
Calcule a densidade de energia num ponto da região sem dielétrico após ligarmos as placas do capacitor a uma bateria com uma diferença de potencial igual a . Forneça sua resposta em função de e

Dois capacitores de placas paralelas, com a mesma separação entre as placas, mas com capacitâncias diferentes, são ligados em paralelo a uma bateria. Ambos os capacitores são preenchidos com ar. A grandeza que NÃO é a mesma para os dois capacitores quando eles estão completamente carregados é:

1. A diferença de potencial;
2. A densidade de energia;
3. O campo elétrico entre as placas;
4. A carga na placa positiva;
5. A constante dielétrica.

Duas placas condutoras paralelas, de área e separação , estão conectadas a uma bateria que provê uma diferença de potencial . As placas são aproximadas uma da outra, mantendo-se paralelas, até que sua separação seja . Considere que é muito menor do que as dimensões das placas, de forma que elas podem ser tratadas como infinitas.

1. Determine a carga armazenada no capacitor formado pelas placas antes e depois da aproximação.
2. As placas são, então, desligadas da bateria e depois a separação das placas é restaurada ao valor . Qual é a diferença entre a energia potencial eletrostática final e a inicial (antes da aproximação) armazenada no capacitor?

Considere um capacitor constituído por duas cascas metálicas cilíndricas e coaxiais. A casca interna de raio tem carga , e a externa de raio tem carga . O comprimento das cascas é muito maior que seus raios ( e ). Expresse as respostas às questões abaixo em termos de , , , e .

(a) Calcule o campo elétrico na região entre as placas.

(b) Calcule a capacitância do capacitor.

(c) Qual é a energia total armazenada no capacitor?

(d) Qual é a densidade de energia elétrica em um ponto qualquer entre as placas?

(e) A partir do resultado da letra (d) obtenha novamente o resultado da letra (c).

Um capacitor de placas paralelas, inicialmente sem dielétrico, tem área e separação entre as placas . O capacitor é carregado por uma bateria de e depois desconectado.

Suponha que a carga no capacitor mantenha-se constante. Em seguida um dielétrico de constante dielétrica é introduzido entre as placas do mesmo.

Considere as seguintes afirmativas

A capacitância do capacitor, com o dielétrico, é .

A carga total do capacitor após o carregamento é .

A energia total do capacitor decresce após a introdução do dielétrico.

O campo elétrico no interior do capacitor diminui após a introdução do dielétrico.

A ddp entre as placas do capacitor decresce após a introdução do dielétrico.

A ddp entre as placas do capacitor aumenta após a introdução do dielétrico.

As afirmativas verdadeiras são:

;

;

;

;

;

;

;

;

Um capacitor de placas planas e paralelas possui inicialmente vácuo entre suas placas, como mostrado na figura abaixo (painel à esquerda). Ele é carregado por uma bateria que fornece uma diferença de potencial constante entre as placas.

A seguir, mantendo a bateria conectada, insere-se no capacitor um material dielétrico de constante dielétrica e espessura igual à metade da distância entre as placas, como mostrado no painel direito da figura abaixo.

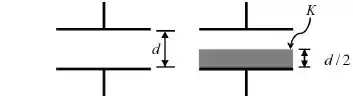
A razão entre as energias armazenadas pelo capacitor depois e antes da inserção do dielétrico vale:

.

.

.

.

.

.

A figura ao lado ilustra um capacitor de placas esféricas de raios e , com .

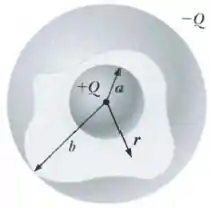
A placa interna tem carga e a placa externa uma carga , com . Há vácuo entre as placas metálicas e a permissividade elétrica do vácuo é denotada por .

Determine o módulo do campo elétrico na região interna do capacitor, , onde é a distância ao centro do capacitor.

Calcule a diferença de potencial entre as placas do capacitor.

Determine a capacitância do capacitor.

Calcule a energia elétrica armazenada no capacitor.

Se a região entre as placas do capacitor for totalmente preenchida com um dielétrico de constante dielétrica , qual é o valor da nova capacitância?

Qual é o valor da diferença de potencial entre as placas do capacitor após a introdução do dielétrico?

Um capacitor é constituído de cilindro com raio e carga coaxial com uma casca cilíndrica fina de raio e carga . O cilindro e a casca cilíndrica têm ambos altura , conforme a figura .

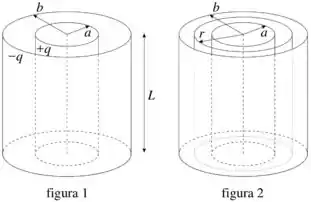
(a) Calcule o vetor campo elétrico dentro do capacitor, na região . Despreze efeitos de borda.

(b) Calcule a capacitância do capacitor.

(c) Calcule a energia contida no interior de um cilindro de raio () e altura , coaxial com o capacitor, conforme a figura .

Qual das afirmações abaixo é verdadeira?

A capacitância de um capacitor, por definição, é a quantidade total de carga que ele pode acumular.

Ao variarmos a diferença de potencial entre as placas de um capacitor dado, fixo, de placas paralelas, variamos a sua capacitância.

Para um capacitor dado, fixo, de placas paralelas, ao dobrarmos a carga em cada placa, dobramos a sua capacitância.

A capacitância de um capacitor dado, fixo, aumenta, quando inserimos algum material isolante entre suas placas, todo o resto mantendo-se inalterado.

Ao dobrarmos a carga armazenada em um dado capacitor, também dobramos a energia armazenada nele.

Dois capacitores idênticos, inicialmente no vácuo, são conectados aos terminais de uma bateria que fornece uma diferença de potencial constante , como mostrado na figura abaixo. A seguir, mantendo a bateria conectada, insere-se uma placa isolante de constante dielétrica entre as placas de um dos capacitores, de forma a ocupar todo o volume entre elas. Nessa situação, é correto afirmar que, após a inserção:

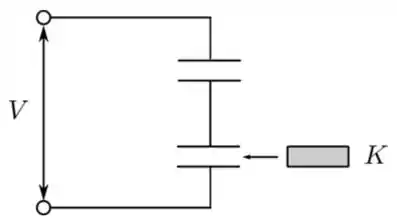
1. A carga armazenada no capacitor com o dielétrico diminui com relação ao valor original.
2. Os dois capacitores armazenam a mesma energia.
3. A carga armazenada no capacitor que permanece no vácuo aumenta com relação ao valor original.
4. Os dois capacitores terão a mesma diferença de potencial entre suas placas.
5. A energia armazenada no capacitor que permanece no vácuo diminui com relação ao valor original.

Um capacitor de placas planas e paralelas encontra-se carregado e armazena inicialmente uma energia . A seguir, deseja-se inserir um material dielétrico no capacitor, de forma a ocupar todo o volume entre as placas. A inserção pode ser feita de duas formas diferentes:

1. A inserção é feita com o capacitor mantido isolado, de forma que a carga armazenada nele permanece inalterada.
2. A inserção é feita com o capacitor conectado a uma bateria que fornece uma diferença de potencial constante entre as placas.

Sejam e as energias armazenadas no capacitor após a inserção do dielétrico pelas formas e , respectivamente. Podemos afirmar que:

Qual das seguintes afirmativas é falsa?

a) No processo de carregamento de um capacitor, cria-se um campo elétrico entre suas placas

b) O trabalho necessário para carregar um capacitor pode ser pensado como sendo o trabalho necessário para criar um campo elétrico entre suas placas.

c) A densidade de energia no espaço entre as placas de um capacitor é diretamente proporcional ao módulo do campo elétrico

d) A diferença de potencial entre as placas de um capacitor é diretamente proporcional ao módulo do campo elétrico

e) A capacitância de um capacitor não depende da quantidade de carga acumulada nele nem da diferença de potencial aplicada nos seus terminais.

13 - Um capacitor de placas paralelas de capacitância é carregado por uma bateria a uma diferença de potencial . Agora, o capacitor é desconectado da bateria e imerso em um recipiente com água destilada de constante dielétrica . Podemos afirmar que:

1. A capacitância aumenta por um fator .
2. A diferença de potencial entre as placas aumenta de um fator .
3. A energia armazenada no capacitor diminui de um fator .

1. I, II e III
2. Apenas I e II
3. Apenas a III
4. Apenas I e III
5. Apenas II

Uma esfera condutora de raio , carregada com carga , está cercada por uma camada condutora esférica concêntrica de raio , carregada com carga . O espaço entre e está preenchido com um material dielétrico de constante dielétrica . O espaço entre e é vácuo. Determine:

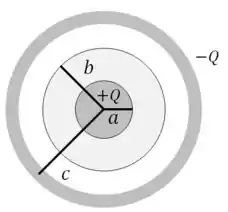
a) O vetor campo elétrico para:

i.

ii.

iii.

b) A diferença de potencial entre e , ou seja .

c) A capacitância do conjunto.

Três capacitores de placas planas e paralelas estão ligados como mostra a figura abaixo. Inicialmente, os capacitores e estão descarregados e está carregado com carga . A chave é então fechada.

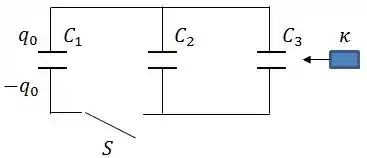
Calcular a carga em cada capacitor e a diferença de potencial através dos mesmos após o estabelecimento do equilíbrio.

Mantendo-se a chave fechada é inserido um material de constante dielétrica no capacitor , preenchendo totalmente o volume entre suas placas.

Nesta nova situação, calcular a carga em cada capacitor e a diferença de potencial através dos mesmos, após o restabelecimento do equilíbrio.

Calcular a variação da energia potencial elétrica em , onde é a energia antes do fechamento da chave e é a energia após a colocação do dielétrico.

Um capacitor de placas paralelas, de área e separação , é originalmente carregado com carga . Desligando—se a bateria, uma lâmina dielétrica de espessura e constante dielétrica é, então, inserida entre as placas do capacitor.

Calcule:

O vetor no interior do dielétrico;

A capacitância desde capacitor;

A diferença de potencial entre as placas do capacitor;

O valor da densidade superficial de carga induzida nas paredes do dielétrico.

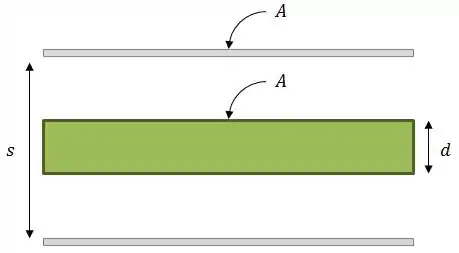
Um capacitor é composto de placas paralelas quadradas de lado e separadas por uma distância . Um bloco de material dielétrico, também de lado e espessura e de constante de permissividade é introduzido no capacitor, preenchendo completamente o espaço entre as placas.

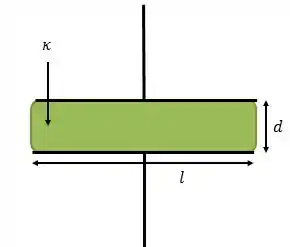
1. Escreva as expressões para as capacitâncias para a situação de vácuo entre as placas (sem o dielétrico) e quanto tem-se o dielétrico de constante de permissividade ;
2. Calcule a variação (devido à colocação do dielétrico) de energia armazenada no caso das placas, quando a carga, nas placas da armadura é mantida constante;
3. Calcule a mudança de energia armazenada (devido à colocação do dielétrico) quando a diferença de potencial entre as placas for mantida constante;
4. Por fim, a placa é parcialmente deslocada, deixando um comprimento do espaço livre, qual será a nova capacitância?

Um capacitor de placas planas e paralelas (área e separação ) é carregado até atingir uma diferença de potencial e uma carga . Uma placa dielétrica, de constante e espessura , é introduzida entre as placas do capacitor, conforme a figura.

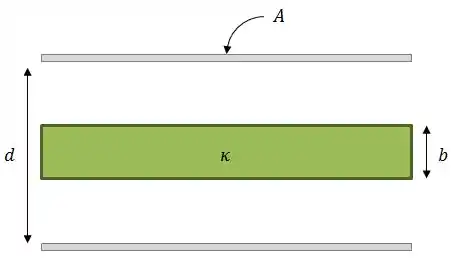
Encontre:

O campo elétrico no espaço vazio situado entre as placas do capacitor e a placa do dielétrico;

O campo elétrico dentro da placa dielétrica;

A diferença de potencial entre as placas do capacitor depois da introdução da placa dielétrica;

A capacidade do capacitor, depois da introdução da placa dielétrica, em função de , , e a permissividade ;

1. Um capacitor de placas paralelas com área de cada placa e separação entre elas , está imerso no vácuo. Calcule a capacitância deste capacitor.
2. Uma placa de material dielétrico com constante dielétrica , espessura e área , é colocada no interior do capacitor, a meia distância de cada uma das placas do mesmo, de maneira que nenhuma fração do dielétrico fique fora do capacitor. Calcule a nova capacitância do capacitor.

(Cap 25 Ex- 51) Um capacitor de placas paralelas tem uma capacitância de , uma área das placas de e um dielétrico de mica () que preenche totalmente o espaço entre as placas. Para uma diferença de potencial de 50 V, calcule (a) o módulo E do campo elétrico no interior do dielétrico; (b) o valor absoluto da carga livre nas placas; (c) o valor absoluto da densidade superficial de cargas induzidas no dielétrico .

(Cap 25 Ex- 54) Duas placas paralela$ de 100 crn 2 de área recebem cargas de mesmo valor absoluto, 8,9 X 10- 1 C, e sinais opostos. O campo elétrico no interior do dielétrico que preenche o espaço entre as placas é 1,4 X 10 6 V/m. (a) Calcule a constante dielétrica do material. (b) Determine o módulo da carga induzida nas superfícies do dielétrico.

(Cap 25 Ex- 53) Um capacitor de placas paralelas tem uma área das placas de e uma distância entre as placas de . Uma bateria é usada para carregar as placas com uma diferença de potencial de e em seguida é removida do circuito. Um dielétrico com de espessura e constante dielétrica é introduzido simetricamente entre as placas. (a) Qual é a capacitância antes da introdução do dielétrico? (b) Qual é a capacitância após a introdução do dielétrico? (c) Qual é a carga das placas antes da introdução do dielétrico? (d) Qual é a carga das placas após a introdução do dielétrico? (e) Qual é o módulo do campo elétrico no espaço entre as placas e o dielétrico? (f) Qual é o módulo do campo elétrico no interior do dielétrico? (g) Qual é a diferença de potencial entre as placas após a introdução do dielétrico? (h) Qual é o trabalho necessário para introduzir o dielétrico?

Três capacitores , e , todos de mesma capacitância, são ligados a uma bateria, como mostrado.

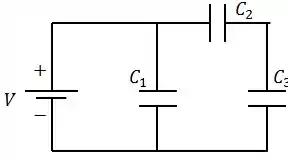
Qual capacitor armazena a maior energia?

;

;

;

ou ;

Todos os capacitores armazenam a mesma energia;

Um capacitor de placas planas e paralelas de área e separação preenchido, em uma metade, com um isolante de constante dielétrica , conforme mostra a figura abaixo. Nessa situação, a diferença de potencial entre as placas vale . Considere que é muito menor que as dimensões das placas e que o sistema se encontra em equilíbrio eletrostático.

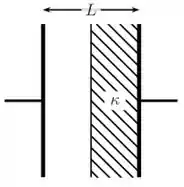
(a) Determine a capacitância do sistema.

(b) Determine a intensidade do campo elétrico no interior do capacitor nas regiões com e sem o isolante.

15ª questão - Um capacitor de é descarregado através de um resistor de . Quanto tempo levará para o capacitor perder metade de sua energia inicial armazenada?

A)

B)

C)

D)

E)

Um capacitor de placas planas e paralelas, imersas no vácuo, é conectado a uma bateria de força eletromotriz constante. Se a distancia entre as placas do capacitor é duplicada enquanto o capacitor permanece conectado a bateria, a energia armazenada no capacitor:

1. Quadruplica
2. Duplica
3. Não se altera
4. Reduz-se a metade
5. Reduz-se a um quarto

Na figura, representamos um gráfico do potencial elétrico entre duas placas planas, paralelas e extensas, uniformemente carregadas com cargas de sinais opostos, conforme medido ao longo da direção ortogonal às placas, sendo uma das placas escolhida como tendo potencial e posição nulos. Qual é o vetor campo elétrico em qualquer ponto entre as placas?

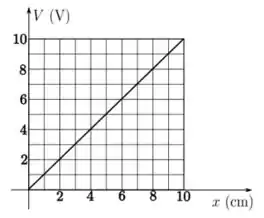
a) .

b) .

c) .

d) .

e) .

Um capacitor de placas planas e paralelas está parcialmente preenchido por um material isolante de constante dielétrica K1 = 3 que possui espessura d igual à metade da separação entre as placas (2d), como mostra a figura abaixo. Em seguida, com a diferença de potencial entre as placas mantida constante por uma bateria, o material isolante é substituído por um outro, que possui constante dielétrica K2 = 2 e que ocupa totalmente o espaço entre as placas. Qual é a razão U1/U2 entre as energias armazenadas pelo capacitor antes e depois da mudança do dielétrico?

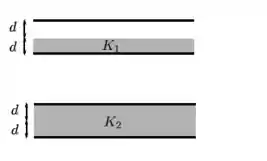
(a) 3/4

(b) 4/3

(c) 4

(d) 1/4

(e) 2/3

(f) 3/2

(g) 1

O potencial elétrico no interior de um capacitor de placas paralelas:

a) é constante.

b) aumenta linearmente da placa positiva para a placa negativa.

c) diminui linearmente da placa positiva para a placa negativa.

d) diminui linearmente da placa negativa para a placa positiva.

e) diminui inversamente com o quadrado da distância à placa negativa.

A figura abaixo mostra o gráfico do potencial elétrico no interior de um capacitor de placas condutoras planas e paralelas posicionadas em e. Considere que é muito menor que as dimensões das placas e que o sistema está em equilíbrio eletrostático. Sabendo que a região (II) está preenchida por vácuo, podemos afirmar que a região (I) está preenchida por um material isolante de constante dielétrica igual a:

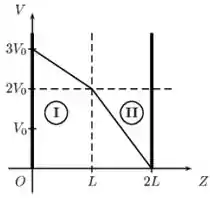
(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

Qual das seguintes afirmativas é falsa?

No processo de carregamento de um capacitor, cria-se um campo elétrico entre suas placas.

O trabalho necessário para carregar um capacitor pode ser pensado como sendo o trabalho necessário para criar um campo elétrico entre suas placas.

A densidade de energia no espaço entre as placas de um capacitor é diretamente proporcional ao módulo do campo elétrico.

A diferença de potencial entre as placas de um capacitor é diretamente proporcional ao módulo do campo elétrico.

Nenhuma das afirmativas anteriores é falsa.

Um capacitor cilíndrico é constituído por duas cascas cilíndricas metálicas e coaxiais. A casca interna possui raio e carga , enquanto que a casca externa possui raio e carga . Ambas as cascas possuem comprimento .

Calcule a capacitância do capacitor.

Calcule a densidade de energia eletrostática armazenada no interior do capacitor.

Utilize o campo elétrico obtido no item , e calcule a energia armazenada no interior do capacitor.

Um dielétrico de constante dielétrica é colocado entre as placas do capacitor de maneira a preencher todo espaço entre elas. Nestas circunstâncias, calcule o campo elétrico no interior do capacitor e as cargas induzidas na superfície do dielétrico, .

Um capacitor de placas planas e paralelas, de capacitância , inicialmente descarregado é conectado a uma fonte de tensão contínua . No instante a chave é fechada e o capacitor fica ligado por um tempo muito longo acumulando uma carga e uma energia potencial (situação em equilíbrio)

Caso 1:

Com a fonte de tensão ligada, um material de constante dielétrica é inserido entre as placas do capacitor. Nestas condições:

1. Demonstre que , onde é a nova energia potencial após a inserção do dielétrico.

Caso 2:

Partindo da situação de equilíbrio, antes de colocar o material de constante dielétrica o capacitor é desligado da fonte de tensão. Em seguida o material dielétrico é então inserido no capacitor mantendo ele desconectado da fonte.

2. Demonstre que , onde é a nova energia potencial após a inserção do dielétrico.

Qual das seguintes afirmativas é falsa?

1. No processo de carregamento de um capacitor, cria-se um campo elétrico entre suas placas.
2. O trabalho necessário para se carregar um capacitor pode ser pensado como o trabalho necessário para se criar um campo elétrico entre suas placas
3. A densidade de energia na região entre as placas de um capacitor depende linearmente do módulo do campo elétrico
4. A diferença de potencial entre as placas de um capacitor plano paralelo depende linearmente do módulo do campo elétrico
5. Ao dobrarmos a carga em cada uma das placas de um capacitor dado, dobramos a diferença de potencial entre suas placas

Uma bateria de é conectada a uma arranjo com dois capacitores de e associados em paralelo conforme a figura. A energia armazenada nos capacitores vale: