Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 24.1 - Ex. 20

As cargas nas placas de um capacitor de 10   μ F são ± 4,0   µ C .

(a) Quanta energia está armazenada no capacitor?

(b) Se a carga é transferida até que seja atingido o valor de ± 2,0   µ C nas placas, quanta energia permanece armazenada?

Passo 1

Cara... Imagina um capacitor comum de capacitância C ...

Quando aplicamos uma diferença de potencial V entre as placas...

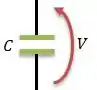
Surgem em cima do capacitor, cargas positivas Q + e em baixo Q - ...

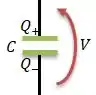
E de acordo com a nossa teoria, essas três grandezas (carga Q , tensão V e capacitância C ) se relacionam por...

Q = C V

A energia pode então ser calculada por...

U = 1 2 C V 2

Ou ainda, juntando as duas equações...

U = 1 2 Q 2 C  

“Tá, mas quem é Q ? É Q - ou Q + ?”

Passo 2

Ora... As duas são iguais em módulo...

Q + = Q -

E é esse módulo que é Q ...

Q = Q + = Q -

Na prática, como o módulo da carga positiva é ela mesma ( Q + = Q + ) então, podemos considerar Q = Q + , saca?

Então no nosso caso, vamos considerar...

Q = + 4,0   μ C = 4 ⋅ 10 - 6   C

Passo 3

L e t r a   A :

Agora é só botar a mão na massa e calcular o valor da energia U ...

U = 1 2 Q 2 C   →

U = 1 2 4 ⋅ 10 - 6 2 10   μ F   →

Como μ = 10 - 6 ...

U = 1 2 16 ⋅ 10 - 12 10 ⋅ 10 - 6   →

U = 8 10 ⋅ 10 - 6   →

U = 0,8 ⋅ 10 - 6   →

Como 10 - 6 é o mesmo que nano ( μ )...

U = 0,8   μ J

Passo 4

L e t r a   B :

Bem... Repare que a expressão da energia no capacitor nos diz que...

U = 1 2 Q 2 C

Então, se a carga nova Q n o v a após a transferência é a metade da carga Q = 4   μ C , isto é Q n o v a = Q / 2 = 2 μ C , então a nova energia armazenada no capacitor após essa transferência será de...

U n o v a = 1 2 Q n o v a 2 C   →

U n o v a = 1 2 Q 2 2 C   →

U n o v a = 1 4 ⋅ 1 2 Q 2 C   →

U n o v a = 1 4 ⋅ U

Ou seja, a energia armazenada cai para 1 / 4 da energia antiga na placa originalmente. Como a energia original U = 0,8   μ J , então...

U n o v a = 1 4 ⋅ 0,8 = 0,2   μ J

Resposta

Letra A:

0,8   μ J

Letra B:

0,2   μ J

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

46 . Um capacitor com placas paralelas no ar é constituído por duas placas quadradas, com um mesmo lado de 12c m e separadas por uma distância igual a 3,7m m . Ele é conectado a uma bateria de 12V . (
33 . Um capacitor de 12,5μ F é conectado a uma fonte de emergia que mantém constante uma diferença de potencial de 24,0V através das placas. Um pedaço de material com constante dielétrica de 3,75 é co
38 . Potencial em células humanas. Algumas paredes celulares no corpo humano possuem uma camada de carga negativa na superfície interior e uma camada de carga positiva de mesmo módulo na superfície ex
71 . Você está realizando experiências com um capacitor plano de placas paralelas com ar entre as placas. Você conecta o capacitor a uma bateria com tensão elétrica igual a 24,0V . Inicialmente a dist
49 . Um capacitor de 20,0μ F é carregado a uma diferença de potencial de 800V . Em seguida, os terminais do capacitor carregado são ligados aos terminais de um capacitor não carregado de 10,0μ F . Cal