Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 27.8 - Ex. 49
Na Fig. 27-14, suponha que , , e . Se a resistência do voltímetro é , que erro percentual o voltímetro introduz na medida da diferença de potencial entre os terminais de ? Ignore a presença do amperímetro.
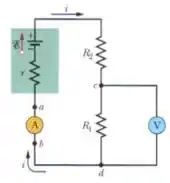
Passo 1
E aí! tudo certinho? 😎
Nesse problema temos um circuito com uma fonte e resistência interna ligado a dois resistores em série e . É conectado um voltímetro no resistor e a resistência interna do voltímetro é . A partir daí queremos saber qual o erro percentual da leitura do voltímetro a partir dessa resistência.
Tem ideia de como fazer isso? 👀
Podemos primeiramente calcular a tensão no resistor antes de conectar o voltímetro e depois de conectar o voltímetro, considerando o voltímetro como uma resistência .
E a partir desses valores, obter o erro percentual...
Saca só! 😉
Passo 2
Primeiro vamos calcular a tensão no resistor com o voltímetro conectado...
Aplicando a regra das malhas na malha da esquerda temos a seguinte equação:
Primeiramente, podemos notar que a corrente que passa no voltímetro é , portanto:
colocando a corrente em evidência:
Aplicando na primeira equação:
Portanto:
A leitura no multímetro é :
Dessa forma:
Tranquilo até aqui? 😁
Passo 3
No caso em que não temos o multímetro, podemos fazer , aplicando l'hôpital tomando como variável :
Dessa forma o erro percentual é:
E aí! o que achou? Responde Aí! 😎
