Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 27.8 - Ex. 55
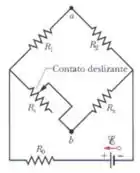
Na Fig. 27-61, o valor de , pode ser ajustado através de um contato deslizante até que os potenciais dos pontos e sejam iguais. (Um teste para verificar se essa condição foi satisfeita é ligar temporariamente um amperímetro sensível entre os pontos e ; se os potenciais dos dois pontos forem iguais, a indicação do amperímetro será zero.) Mostre que quando esta condição é satisfeita, . Uma resistência desconhecida ( pode ser medida em termos de uma resistência de referência () usando este circuito, conhecido como ponte de Wheatstone.
Passo 1
E aí, galerinha! 😁
Nesse problema temos que formar uma ponte de Wheatstone a partir do circuito dado no enunciado e provar que quando a ponte está perfeitamente equilibrada, temos que
Tem ideia de como fazemos isso? 👀
Vamos considerar a corrente , sendo aquela que passa pelos resistores 1 e 2. Vamos definir que a corrente é positiva quando está indo para a direita. Também, vamos definir a corrente que passa pelos resistores e com sentido para a direita. Dessa forma, temos que a lei das malhas nos dá:
Veja só! 😉
Passo 2
Como dito pelo enunciado o potencial é o mesmo nos pontos e , a diferença de potencial em cima de é igual a diferença de potencial em cima de :
Assim:
Manipulando essa equação, chegamos em
Entendeu tudo? Responde Aí! 😉
