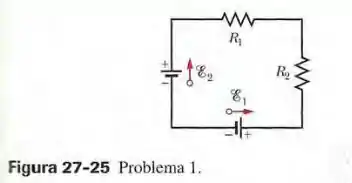
Na Fig. 27-25 , as fontes ideais têm forças eletromotrizes e e os resistores têm resistências e. Determine (a) a corrente no circuito; (b) a potência dissipada no resistor l; ( c) a potência dissipada no resistor 2; ( d) a potência fornecida pela fonte l ; (e) a potência fornecida pela fonte 2. (f) A fonte l está fornecendo ou recebendo energia? (g) A fonte 2 está fornecendo ou recebendo energia?

(a)Seja i a corrente no circuito e vamos tomar como positivo o sentido para a esquerda em

. De acordo com a regra das malhas,. Explicitando i, temos:

Como o valor calculado é positivo, o sentido da corrente é o sentido anti-horário.

(b)De acordo com a Eq. 26-27, se i é a corrente em um resistor R, a potência dissipada pelo resistor é dada por

(C)

(d)De acordo com a Eq. 26-26, se i é a corrente em uma fonte de fem ℰ, P = i ℰ é a potência fornecida pela fonte se a corrente e a fem têm o mesmo sentido, e é a potência absorvida pela fonte, se a corrente e a fem têm sentidos opostos.

(e)

(f)Como, no caso da fonte 1, a corrente tem o mesmo sentido que a fem, a fonte 1 está fornecendo energia ao circuito.

(g)Como, no caso da fonte 2, a corrente e a fem têm sentidos opostos, a fonte 2 está recebendo energia do circuito.