Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 27.6 - Ex. 12
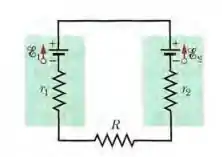
(a) Na Fig. 27-28, qual deve ser o valor de R para que a corrente no circuito seja 1,0 mA? Sabe-se que , ,. (b) Qual é a potência dissipada em ?
Passo 1
Shooow galerinha, vamos continuar?
Aqui deveremos encontrar o valor de para que a corrente que atravessa o circuito seja 1 mA.
Bom, primeiro nós devemos lembrar que pela Lei de tensão de Kirchhoff, a tensão total em torno de qualquer ciclo será a soma de toda a queda de tensão individual deve ser igual à zero:
Passo 2
Isolando a resistência que queremos achar na letra (a):
Sabendo que:
Substituindo:
Bora achar a letra (b) ??
Passo 3
A letra (b) nos pede a potência dissipada em , e como achamos?
Mais uma equaçãozinha bem massa:
Se já sabemos os valores é só substituir:
Isso aí !! Chegamos ao fim de mais uma
Resposta
(a)
(b)
Exercícios de Livros Relacionados
No circuito indicado na Figura P25.66, R é um resistor variável, cujo valor pode variar de 0 a , e a e b são os terminais de uma bateria com fem E 15,0 V e uma resistência interna de 4,00 V. O amperím
Um resistor externo R está ligado entre os terminais de uma bateria. O valor de R varia. Para cada valor de R, a corrente I no circuito e a voltagem nos terminais da bateria Vab são medidos. Os result
Em um motor cc com as bobinas de campo e o rotor conectados em paralelo (Figura E27.47), a resistência Rf das bobinas de campo é 106 V e a resistência Rr do rotor é 5,9 V. Quando uma diferença de pote
Um dispositivo de fem E fornece potência a uma linha de transmissão cuja resistência é R. Determine a razão entre a potência dissipada na linha para E=110.000V e a potência dissipada para E = 110V, co
Na Fig. 29-6a, determine a diferença de potencial entre os terminais de R2 para E = 12 V, R1 = 3,0 Ω , R2 = 4,0 Ω e R3 = 5,0 Ω .