Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 30.Problemas Adicionais - Ex. 100
A Fig. 30-78 mostra um fio em forma de arco de circunferência de raio , com centro no ponto O. Um fio retilíneo pode girar em torno do ponto e faz um contato deslizante com o arco no ponto . Outro fio retilíneo completa o circuito. Os três fios têm uma área da seção reta de e uma resistividade de, e o circuito está em uma região onde existe um campo magnético, de módulo , que aponta para fora do papel. O fio parte do repouso na posição e passa a se mover com uma aceleração angular constante de . Determine, em função de , em radianos,
(a) a resistência do circuito e
(b) o fluxo magnético que atravessa o circuito.
(c) Para qual valor de a corrente induzida no circuito é máxima?
(d) Qual é a corrente máxima induzida no circuito?
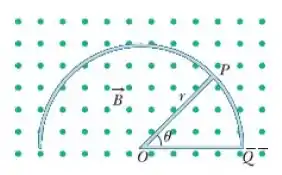
Passo 1
Os dados que o problema nos trás são os seguintes:
Daí das equações de movimento angular, com velocidade angular inicial zero e posição angular inicial também zero temos:
Certo? Guarda esses dados! Vamos usar num futuro muito próximo! Beleza? Vamos pra letra a então!
Passo 2
Letra a:
Como os fios estão ligados em sequência a resistência total vai ser a soma das resistências das partes individuais dos fios. Da definição de resistência temos:
A resistividade é igual para todas as partes, bem como a área da seção reta. Assim:
O comprimento dos fios e são constantes e valem . Já o arco depende do ângulo :
Agora vamos substituir os valores de :
Passo 3
Letra b:
O fluxo magnético é dado pela quantidade de linhas de campo que atravessam uma determinada área, não é? Então, quando o fio começa a se movimentar, ele acaba fechando o circuito e formando uma espira. E a área dessa espira aumenta confirme vai se movimentando. Assim a área e o fluxo magnético vão depender do ângulo.
A área vai ser a de um setor circular, assim fazendo uma regra de três simples temos:
E o fluxo magnético é:
Como o vetor normal à área e o campo magnético tem a mesma orientação temos que , então o fluxo é:
E substituindo os valores do campo e do raio temos:
Show! Vamos pra próxima letra?
Passo 4
Letra c:
Como falei ali no passo anterior, a área da espira é dependente do ângulo então ali vai aparecer uma força eletromotriz induzida! Daí pra determinar a corrente vamos usar a Lei de Faraday:
Mas você se pergunta: onde está a corrente? Daí do lado direito vamos usar a Lei de Ohm:
Pronto! Temos aqui nossa equação! O fluxo depende de e lembrando que a resistência também é (achamos ela no passo 2), agora é só substituir as expressões e derivar do lado esquerdo, borá lá?
Como apenas é dependente do tempo, o resto do lado esquerdo pode sair do parênteses:
Agora, para determinar em qual a corrente induzida é máxima temos que derivar essa corrente e igualar a zero:
Aqui vou usar a regra do quociente, saca só
Parece que ficou feio, não é? Mas é assim mesmo! Daqui a pouco as coisas vão se resolver, saca só. Passando o denominador pro outro lado multiplicando ele zera, pois temos um do lado direito da equação, assim ficamos só com o numerador:
Daí conseguimos cancelar dos dois lados:
E agora vamos lá no passo 1 resgatar os valores de do passo 1:
Passando tudo para o mesmo lado e igualando a zero temos:
Olha só! Chegamos a uma equação de segunda ordem em . Agora ficou tranquilo de resolver!
Resgatando o valor de do passo 1:
Mas como queremos apenas a solução positiva: e o valor de é:
Passo 5
Letra d:
E a corrente máxima vai ser quando , ou quando . Do passo anterior encontramos uma expressão para a corrente induzida, vai lá dar uma espiadela (logo antes de derivarmos a expressão):
E sabendo as expressões de e temos:
Agora é só substiuir os valores:
O sinal indica que é oposto ao sentido positivo da corrente no circuito =)