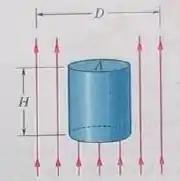
Na Fig. 33-38, o feixe de um laser com 4,6 W de potência e D=2,60m m de diâmetro é apontado para cima, perpendicularmente a uma das faces circulares (com menos de 2,6 m m de diâmetro) de um cilindro perfeitamente refletor, que é mantido suspenso pela pressão da radiação do laser. A massa específica do cilindro é 1,20g / c m 3 . Qual é a altura H do cilindro?

Portanto, a altura do cilindro é de 4.91 × 10 - 7 m .

Enunciado

Falaiii meus xuxu’s, ceis tão bonzinho??

Espero que sim hein, bora lá pra mais uma?

Encostaaaa

Vamos escrever a expressão para a massa do cilindro em termos de sua altura H, diâmetro D e a densidade , como mostrado a seguir

No caso dado, a força de radiação F atua no sentido ascendente e a gravidade g atua no sentido descendente.

Vamos expressar a segunda lei de Newton no estado do sistema está em equilíbrio.

No caso de superfície perfeitamente refletora, uma expressão para a força radiante é,

Onde,

é a intensidade

é a área

é a velocidade da radiação

Vamos escrever para a área da seção transversal do cilindro

Substituindo por m, e por F, na equação

Logo:

Vamos reorganizar

A intensidade é expressad como potência (P) por área da seção transversal do cilindro como:

Substiutindo (1)

Agora iremos fazer as substituições numéricas

Portanto, a altura do cilindro é de .

Portanto, a altura do cilindro é de