Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 34.3 - Ex. 39
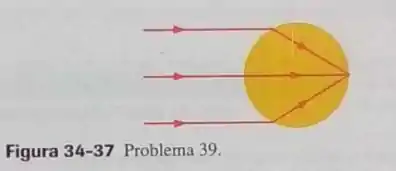
Na Fig. 34-37, um feixe de raios luminosos paralelos produzido por um laser incide em uma esfera maciça transparente de índice de refração . Se uma imagem pontual é produzida na superfície posterior da esfera qual é o índice de refração da esfera? Existe algum valor do índice de refração para o qual é produzida uma imagem pontual no centro da esfera? Se a resposta for afirmativa, qual é esse valor?
Passo 1
Bom, a figura dada no problema vai nos ajudar a encontrar a resposta da letra (a), como a imagem é formada no ‘fundo da esfera’, a gente pode dizer que já que os raios precisam ultrapassar toda a esfera para chegar na imagem (se olharmos para o raio do meio fica mais fácil de entender isso).
Outra coisa q a gente pode dizer é que a distância do objeto em relação à esfera é infinita , já que os raios vêm de um laser que está muito longe da esfera. E como o índice de refração do meio 1 é o ar, temos tudo que precisamos para calcular o índice da esfera.
Passo 2
Podemos chegar na resposta pela equação de superfícies refratoras esféricas:
Isolando :
Substituindo o que a gente havia analisado no passo 1:
Passo 3
Na letra (b) a questão pede o índice de novo, mas agora a imagem tem que estar no centro da esfera, o que significa que , e os outros valores ficam os mesmos que usamos para resolver a letra (a), então:
Mas como dá para ver, a equação acima resulta em o que significa que não tem como focalizarmos os raios luminosos do laser no centro da esfera, então não é possível colocar a imagem lá.