Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 5.9 - Ex. 45
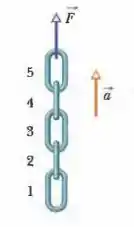
Na Fig. 5-43, uma corrente composta por cinco elos, cada um de massa , é erguida verticalmente com uma aceleração constante de módulo . Determine o módulo (a) da força exercida pelo elo sobre o elo , (b) da força exercida pelo elo sobre o elo , (c) da força exercida pelo elo sobre o elo e (d) da força exercida pelo elo sobre o elo . Determine o módulo (e) da força exercida pela pessoa que está levantando a corrente sobre o elo e (f) a força resultante que acelera cada elo.
Passo 1
Vamos láááá!!!
Para iniciar esta questão precisamos ter dois conceitos muito bem sólidos. Primeiro, a terceira lei de Newton tem que está no sangue, porque o desenvolvimento desta questão se baseia nela e segundo, a segunda lei de Newton. Então, só para relembrar, a segunda lei de Newton diz:
Considerando que as forças estão na vertical, teremos:
Beleza?!
Já a terceira lei de Newton diz que se um corpo exerce uma dada força em um outro corpo, uma força de módulo igual a que foi realizada atua sobre o corpo que exerceu a força, porém no sentido contrário. Show de bola?!
Nesta questão foi dada a massa de cada elo () e aceleração do conjunto (). A partir disso, vamos determinar as respostas do problema.
Passo 2
Vamos aplicar a segunda lei de Newton para o elo .
Nele somente há o peso vertical para baixo, e a força que o elo faz no elo vertical e para cima. Assim:
Substituindo os valores conhecidos:
Ou seja, a força que o elo faz no elo é de
E podemos determinar o valor da força resultante:
Passo 3
Para o elo 2, teremos atuando sobre ele a força peso para baixo , a força que o elo 3 faz sobre o elo 2 para cima e a força que o elo 1 faz sobre o elo que está para baixo .
Pela terceira lei de newton, temos que o módulo da força que o elo 1 faz sobre o 2 é igual ao módulo da força que o 2 faz sobre o 1, portanto.
Assim, resolvendo a segunda lei, teremos:
Isolando e substituindo os valores conhecidos:
E determinando a força resultante que neste elo:
Passo 4
Para o elo faremos exatamente igual ao elo . Neste elo temos a força agindo vertical para baixo, a força peso agindo vertical para baixo e a força agindo vertical para cima. Assim:
E lembrando que a força é igual a força que calculamos anteriormente.
Isolando e substituindo os valores conhecidos:
E, por fim, a força resultante neste elo:
Passo 5
Para o elo temos a reação da força atuando vertical para baixo, temos a força agindo vertical para cima e o peso vertical para baixo. Portanto:
Onde
Isolando e substituindo os valores conhecidos:
E, determinando a força resultante neste elo:
Passo 6
Para o elo , temos a força atuando vertical para cima, a força agindo vertical para baixo e o peso do elo também vertical para baixo. Assim:
Onde
Isolando e substituindo os valores conhecidos:
E, por último, a força resultante é:
Resposta
- ;
- ;
- ;
- ;
- .