Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 5.9 - Ex. 62
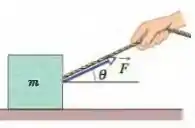
A Fig. 5-45 mostra um bloco de sendo puxado em um piso sem atrito por uma corda que aplica uma força de módulo constante de e um ângulo que varia com o tempo. Quando o ângulo chega a , qual é a taxa de variação da aceleração do bloco se (a)e (b) ? (Sugestão: Transforme os graus em radianos.)
Passo 1
Esta é uma questão de aplicação da segunda lei de Newton. Além disso, para resolver este problema precisamos saber a derivada, pois ele nos pede a taxa de variação da aceleração do bloco e quando falamos em taxa de variação devemos associar a derivada, show?
Inicialmente vamos escrever a segunda lei de Newton para a componente , considerando o eixo paralelo ao chão:
Isolando a aceleração :
Substituindo os valores da massa e da força que são fixos:
Antes de fazer qualquer cálculo, vamos seguir a sugestão do enunciado e transformar de graus para radianos. Para isso, multiplicaremos o valor por um fator de .
Passo 2
Determinando qual o instante que o ângulo é igual a :
Isolando :
Quando o ângulo for negativo, teremos o mesmo valor, porém com negativo.
Passo 3
Substituindo o primeiro valor de na :
Derivando os dois lados em função do tempo:
Substituindo agora o instante calculado no passo anterior:
Passo 4
Agora, de maneira análoga, fazendo para o segundo dado:
Derivando os dois lados em função do tempo:
Substituindo agora o instante calculado:
Resposta
- ;
- .