Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 5.6 - Ex. 12
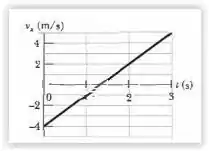
Duas forças horizontais e agem sobre um disco de que desliza sem atrito sobre o gelo, no qual foi desenhado um sistema de coordenadas . A força aponta no sentido positivo do eixo e tem um módulo de . A força tem um módulo de . A Fig. 5-32 mostra a componente da velocidade do disco em função do tempo . Qual é o ângulo entre as orientações constantes das forças e ?
Passo 1
Belezera galerinha, vamos começar achando a aceleração a partir do gráfico.
Como temos um gráfico onde nossa velocidade é representada por uma reta, podemos encontrar a aceleração usando a fórmula:
Pontos escolhidos: (0,-4) e (1,-1)
Ps.:Pode usar quaisquer outros pontos do gráfico.
Passo 2
Vamos agora usar a Segunda Lei de Newton à componente das forças, pois aqui temos a aceleração no eixo x.
Sabemos pelo enunciado que a força é uma força que está no eixo x positivo, por isso, sua componente vai ser ela própria.
E a componente no eixo x da força , vai ser dada por:
Sendo esse o ângulo entre a força e o eixo x.
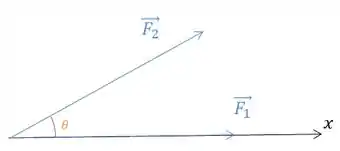
E olha só, esse ângulo também é o ângulo entre as forças que o enunciado pediu pra gente!!Beleza, bora substituir na 2ª lei de Newton!
Tal que:
Portanto: