Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo - Ex.
Na Fig. 7-45, uma corda passa por duas polias ideais. Uma lata de massa está pendurada em uma das polias e uma força é aplicada à extremidade livre da corda. (a) Qual deve ser o módulo de para que a lata seja levantada com velocidade constante? (b) Qual deve ser o deslocamento da corda para que a lata suba ? Durante esse deslocamento, qual é o trabalho realizado sobre a lata (c) pela força aplicada (através da corda) e (d) pela força gravitacional? (Sugestão: quando uma corda é usada da forma mostrada na figura, a força total com a qual a corda puxa a segunda polia é duas vezes maior que a tensão da corda.)
Passo 1
O enunciado nos pede para considerarmos a velocidade com que a lata sobe como constante, portanto, há um equilíbrio de forças na lata. Show? Por isso, a força necessária para levantar a lata deve ser igual ao módulo do peso da lata de maneira que:
O próprio enunciado nos diz que a força com que a corda puxa a segunda polia é duas vezes maior que a tensão na corda. Sendo assim:
Ode a gente pode verificar pela imagem que a tração e a força peso da lata se relacionam como:
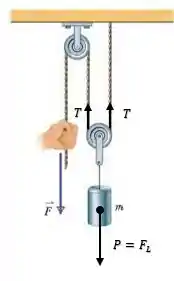
Então substituindo os valores:
Passo 2
Agora olhando para esquerda, para a mão do rapaz que puxa a corda, podemos visualizar que ela quem deve equilibrar a tensão no fio para que a lata se mova com velocidade constante, de forma que:
Portanto, o módulo de deve ser igual a para subir a lata com velocidade constante.
Passo 3
Para determinar o deslocamento da corda, devemos pensar que para a lata subir , as partes da corda que estão à direita e à esquerda da polia da lata, dividem o deslocamento em dois, isso quer dizer que o deslocamento da caixa, é metade do deslocamento da corda, tal que:
E como queremos encontrar o deslocamento da corda, então:
Já que , obtemos que:
Ou voltando para :
Passo 4
Como a força que puxa a corda já foi determinada e é constante, então podemos usar a seguinte relação para determinar o trabalho realizado por ela:
Lembrando que o deslocamento está no sentido da força aplicada, então , de forma que:
Passo 5
De maneira análoga ao passo anterior, a força peso também é constante, então também podemos usar a mesma relação para calcular o trabalho. Entretanto, devemos perceber que o peso age no sentido contrário ao movimento da lata, portanto, e o deslocamento é a metade do deslocamento da extremidade da corda. Assim:
Resposta
- ;
- ;
- ;
- .