Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo - Ex.
A Fig. 8-32 mostra uma haste fina, de comprimento e massa desprezível, que pode girar em torno de uma das extremidades para descrever uma circunferência vertical. Uma bola de massa está presa na outra extremidade. A haste é puxada lateralmente até fazer um ângulo com a vertical e liberada com velocidade inicial . Quando a bola desce até o ponto mais baixo da circunferência, (a) qual é o trabalho realizado sobre a bola pela força gravitacional e (b) qual é a variação da energia potencial do sistema bola-Terra? (c) Se a energia potencial gravitacional é tomada como zero no ponto mais baixo da circunferência, qual é seu valor no momento em que a bola é liberada? (d) Os valores das respostas dos itens de (a) e (c) aumentam, diminuem ou permanecem os mesmos se o ângulo é aumentado?
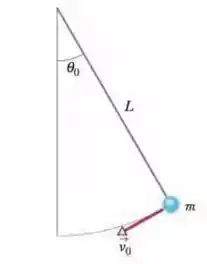
Passo 1
Como a força gravitacional é conservativa, então, podemos calcular o trabalho realizado por ela através do seguinte teorema:
Assim, esquevendo a equação da energia potencial:
A altura inicial da bolinha, considerando o ponto mais baixo como , pode ser calculada por:
Passo 2
Calculando a variação da altura entre o ponto inicial e o ponto mais baixo:
Assim, o trabalho realizado pela força gravitacional entre esses dois pontos é:
Passo 3
Calculamos o trabalho usando a negativa da variação da energia potencial, assim:
Passo 4
A energia potencial da bolinha quando ela é liberada, usando no ponto mais baixo, então:
Passo 5
Se o ângulo aumenta, a altura inicial também aumenta, por isso, em valores absolutos todos os itens anteriores também aumentarão.
Resposta
- ;
- ;
- ;
- .