Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo - Ex.

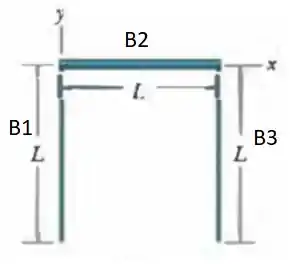
Na Fig. 9-37, três barras finas e uniformes, de comprimento L = 22   c m , formam um U invertido. Cada barra vertical tem uma massa de 14   g ; a barra horizontal tem massa de 42   g . Quais são (a) a coordenada x e (b) a coordenada y do centro de massa do sistema?

Passo 1

Para calcular a coordenada de cada eixo do centro de massa podemos usar as seguintes relações:

x c m = m 1 x 1 + m 2 x 2 + m 3 x 3 m 1 + m 2 + m 3

y c m = m 1 y 1 + m 2 y 2 + m 3 y 3 m 1 + m 2 + m 3

Passo 2

Já temos a massa de cada barra, agora vamos obter as coordenadas do centro de massa de cada barra, para isso vamos estabelecer um eixo referencial:

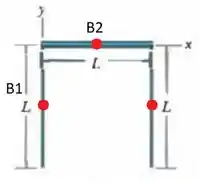
B1

x c m = 0

y c m = - L 2

B2

x c m = L 2

y c m = 0

B3

x c m = L

y c m = - L 2

Passo 3

Agora é só aplicar os dados na fórmula inicial lembrando que L=11:

x c m = m 1 x 1 + m 2 x 2 + m 3 x 3 m 1 + m 2 + m 3

x c m = 14 * 0 + 42 * 11 + 14 * ( - 11 ) 14 + 42 + 14 =11cm

y c m = m 1 y 1 + m 2 y 2 + m 3 y 3 m 1 + m 2 + m 3

y c m = 14 * ( - 11 ) + 42 * 0 + 14 * ( - 11 ) m 1 + m 2 + m 3 = - 4,4 c m

Resposta

  1. x c m = 11   c m ;
  2. y c m = - 4,4   c m .
Ver Outros Exercícios desse livro