Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo - Ex.

Você dirige do Rio a São Paulo metade do tempo a 55   k m / h e a outra metade a 90   k m / h . Na volta, você viaja metade da distância a 55   k m / h e a outra metade a 90   k m / h . Qual é a velocidade escalar média (a) na viagem do Rio a São Paulo, (b) na viagem de São Paulo ao Rio, e (c) na viagem inteira? (d) Qual é a velocidade média na viagem inteira? (e) Plote o gráfico de x em função de   t para o item (a), supondo que o movimento ocorre no sentido positivo de

x . Mostre de que forma a velocidade média pode ser determinada a partir do gráfico.

Passo 1

(a) Para encontrar a velocidade escalar média da viagem Rio – São Paulo v m 1 , precisamos ter em mente que o carro percorre uma distancia s = v . t e que a velocidade escalar média é a razão entre a distância total percorrida e o tempo de viagem T.

v m 1 = ∆ s ∆ t

A distância total percorrida é a soma da distância percorrida a 55   k m / h com a percorrida a 90   k m / h :

∆ s 1 + ∆ s 2 = v 1 T 2   + v 2 T 2

Onde T é o tempo total da viagem. Dessa forma:

v m 1 = v 1 . T 2 + v 2 T 2 T

v m 1 = T 2 v 1 + v 2 T

v m 1 = v 1 + v 2 2

v m 1 = 55   k m / h + 90   k m / h 2

v m 1 = 73   k m / h

Passo 2

(b) No caso da viagem São Paulo – Rio, devemos lembrar que t = S / v .

E agora, viajamos metade da distância a 55   k m / h e a outra metade a 90   k m / h . Portanto, nossa velocidade escalar média será a distância total percorrida dividido pelo tempo total gasto, onde o tempo será a soma dos tempos em cada velocidade:

T = t 1 + t 2

T = S 2 ∙ 1 v 1 + S 2 ∙ 1 v 2

Com isso:

v m 2 = S t 1 + t 2

v m 2 = S S 2 ∙ 1 v 1 + S 2 ∙ 1 v 2

v m 2 = S S ∙ v 2 + S ∙ v 1 2 v 1 v 2

v m 2 = S S ( v 2 + v 1 ) 2 v 1 v 2

Cortando o S e arrumando a fração:

v m 2 = 2 v 1 v 2 v 1 + v 2

v m 2 = 2 ∙ 55 ∙ 90 55 + 90

v m 2 = 68   k m / h

Passo 3

(c) A velocidade escalar média de toda viagem pode ser descoberta usando o mesmo raciocínio do item anterior. Mas, agora, viajamos o dobro da distância entre Rio e São Paulo, sendo que, metade da distância (na ida) estávamos a 73 k m / h e a outra metade (na volta): estávamos a 68 k m / h :

v m t o t a l = 2 S S v m 1 + S v m 2

v m t o t a l = 2 . v m 1 . v m 2 v m 1 + v m 2

v m t o t a l = 2 ∙ 73 ∙ 68 73 + 68

v m t o t a l = 70   k m / h

Passo 4

Para responder a letra d) devemos estar atentos a diferença entre velocidade média escalar e velocidade média. A velocidade escalar média é a razão entre a distância percorrida e o tempo, já a velocidade média é a razão entre o deslocamento e o tempo.

Como o carro volta para seu ponto de origem, seu deslocamento é zero e, portanto:

v m = 0 T

v m = 0 .

Passo 5

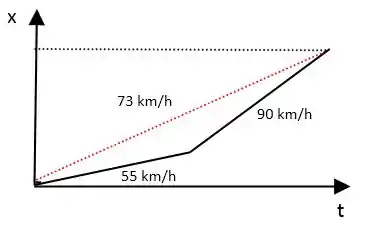
A velocidade média do caso a) pode ser encontrada pela tangente do ângulo de inclinação da reta que liga o ponto inicial ao final, em um plano cartesiano x por t .

Para montar o gráfico de x, precisamos apenas olhar para a equação de s nesses trechos.

Metade foi:

∆ s 1 = v 1 T 2

E a outra metade:

∆ s 2 = v 2 T 2

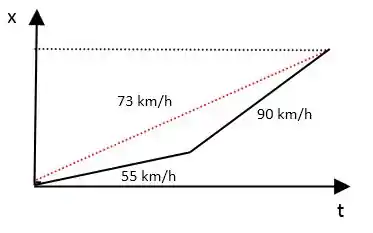
Resposta

a) v e m 1 = 73   k m / h

b) v e m 2 = 68   k m / h

c) v e m ' = 70   k m / h

d) v m = 0

e)

Ver Outros Exercícios desse livro