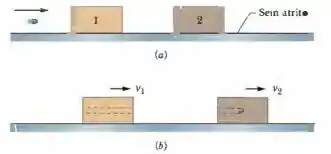
Na Fig. 9-58a, uma bala de é disparada horizontalmente contra dois blocos inicialmente em repouso sobre uma mesa sem atrito. A bala atravessa o bloco 1 (com de massa) e fica alojada no bloco 2 (com de massa). Os blocos terminam com velocidades e (Fig. 9-58b ). Desprezando o material removido do bloco 1 pela bala, encontre a velocidade da bala (a) ao sair do bloco 1 e (b) ao entrar no bloco 2 .
Passo 1
Então galera, primeiramente precisamos definir as condições iniciais do problema .Vamos escolher um eixo horizontal apontando para a direita .
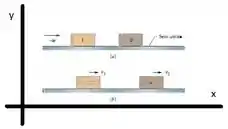
Usando a lei de conservação do momento para relacionar:
Momento 1 - em que a bala está prestes a se chocar com o segundo bloco
Momento 2 - quando a bala fica alojada no segundo bloco
Podemos calcular a velocidade da bala quando ela sai do primeiro bloco:
Passo 2
Usando novamente a lei de conservação do momento , dessa vez para relacionar:
Momento 1 - quando a bala está prestes a se chocar com o primeiro bloco
Momento 2 - quando a bala acabou de atravessar o primeiro bloco e está com a velocidade calculada no item (a).
Podemos calcular a velocidade da bala ao entrar no bloco 1 :
o que nos dá .
Resposta
Tranquilo galera? Bora resolver mais questões então ☺