Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 27.6 - Ex. 21
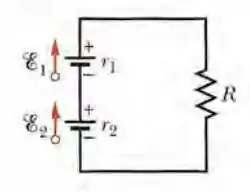
Na Fig. 27-33, a fonte 1 tem uma força eletromotriz " e uma resistência interna e a fonte 2 tem uma força eletromotriz "e uma resistência interna . As fontes são ligadas em série com uma resistência externa R. (a) Qual é o valor de R para o qual a diferença de potencial entre os terminais de uma das fontes é zero? (b) Com qual das duas fontes isso acontece?
Passo 1
Temos uma situação que o circuito que temos duas forças eletromotriz e uma resistencia. Para obter a solução mais geral possível, vamos chamar de e as fem das fontes, embora tenham o mesmo valor. Queremos descobrir aqui qual deve ser o valor de para que a diferença de potencial entre os terminais de alguma fonte seja nula.
Como as fontes estão em série com a mesma polaridade, as fem se somam e a fem total é . A resistência total do circuito é .
Passo 2
(a) A corrente no circuito é
Como a fonte 1 possui uma resistência interna maior, ela é a que pode apresentar uma diferença de potencial zero entre os terminais. Fazendo , obtemos:
Note que, como
Passo 3
(b) A fonte que fica zerada é a . Claro, ela tem maior resistência interna e, à medida que a corrente no circuito aumenta, a queda de tensão na sua resistência interna aumenta mais rapidamente que na fonte que tem menor resistência interna.
Resposta
(a)
(b) Como foi visto no item (a), isso acontece com a fonte 1.