Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 27.6 - Ex. 16
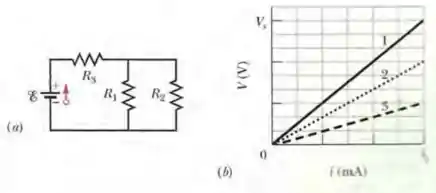
A fonte ideal da Fig. 27-39a tem uma força eletromotriz . A curva da Fig. 27-39b mostra a diferença de potencial entre os terminais do resistor em função da corrente no resistor. A escala do eixo vertical é definida por e a escala do eixo horizontal é definida por . As curvas e são gráficos semelhantes para os resistores e . Qual é a corrente no resistor ?
Passo 1
E aí! como vai? 😉
Nesse problema temos um circuito com duas resistências em paralelo e uma terceira em série a essas. Temos no gráfico (b) a diferença de potencial nas resistências 1, 2 e 3.
A reta 1 tem uma inclinação , a reta 2 tem uma inclinação e a reta 3 tem uma inclinação . A resistência equivalente de e em paralelo é
Como essa resistência está em série com , a resistência equivalente do conjunto é
A partir daí podemos começar o problema...
Veja só! 😉
Passo 2
A corrente que atravessa a bateria é, portanto
e a queda de tensão em é
Subtraindo este valor da tensão da bateria (por causa da regra das malhas), obtemos a tensão entre os terminais de .
A lei de Ohm nos dá a corrente em :
Entendeu tudo? Responde Aí! 😎
Resposta
(a)