Enunciado
Física - Halliday - Vol 3- Ed: 8º - Capítulo 29.Problemas Adicionais - Ex. 81a
A figura 29-86 mostra uma seção reta de um condutor cilíndrico oco de raios e que conduz uma corrente uniformemente distribuída. (a) Mostre que, no intervalo , o módulo do campo elétrico a uma distância do eixo central do condutor é dado por
Passo 1
Fala aí! tudo certinho? 😉
Nesse problema temos um condutor oco de raio interno e raio externo e nosso objetivo é mostrar que para o campo magnético é dado por
Tem ideia de como fazer isso? 👀
A lei de Àmpere é utilizada para determinar o campo magnético total de uma região que apresente algum tipo de simetria. De acordo com ela:
O círculo do sinal de integral indica que a integração do produto escalar deve ser realizada para uma curva fecahda, conhecida como amperiana. A corrente é a corrente total envolvida pela curva fechada. Essa corrente tamém pode ser escrita como:
onde é a densidade de corrente na curva fechada.
Veja só! 😁
Passo 2
Para determinarmos o campo magnético em pontos situados no interior do fio, podemos usar uma amperiana de raio por dentro do fio, conforme a figura abaixo.
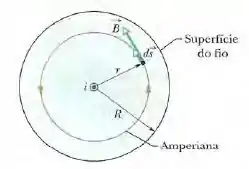
Da lei de Àmpere:
Para calcular o lado direito da lei de Àmpere, observamos que, como a distribuição de corrente é uniforme, a corrente envolvida pela amperiana é proporcional à área envolvida pela curva, ou seja,
Assim,
E é isso! O que achou? Responde Aí! 😉
