Enunciado
Física - Okuno - Física para Ciências Biológicas e Biomédicas- Ed: 1º - Capítulo 14.Problemas - Ex. 1
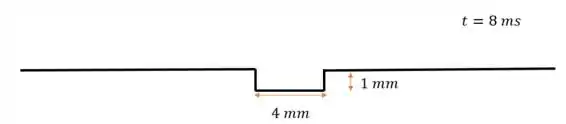
A figura abaixo mostra dois pulsos numa corda tensionada no instante , propagando-se com a velocidade de em sentidos opostos. Faça o gráfico da configuração da corda nos instantes e .
Passo 1
E aíí, suave?
Vamos lá fazer esse exercício!
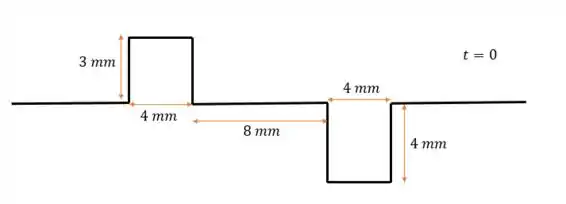
Temos essa imagem:
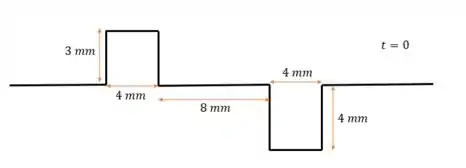
E queremos desenhar a configuração da corda pra diferentes valores de
A primeira coisa que temos que nos atentar é que os pulsos se propagam com velocidade de
Multiplicando em cima e embaixo por , temos:
Então os pulsos se propagam a e é essa velocidade que vamos usar para montar as configurações, bora lá!
Passo 2
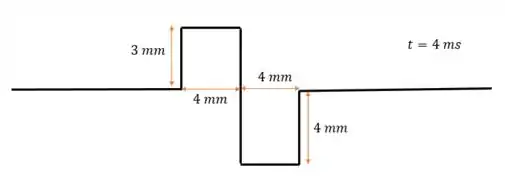
Em o primeiro pulso vai ter se movido para a direita e o segundo vai ter se movido para a esquerda, então temos:
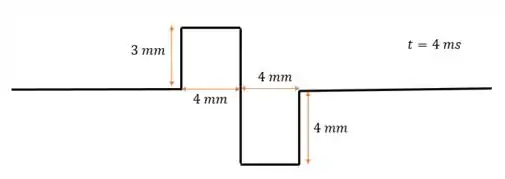
Passo 3
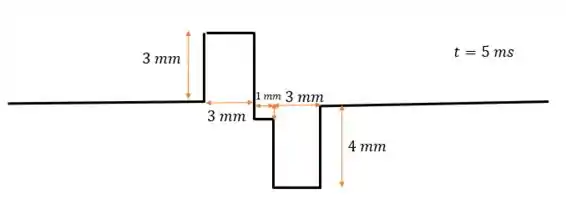
Em , o primeiro pulso vai ter se movido mais para a direita e o segundo mais para a esquerda (quando comparados ao desenho do passo 2), então:
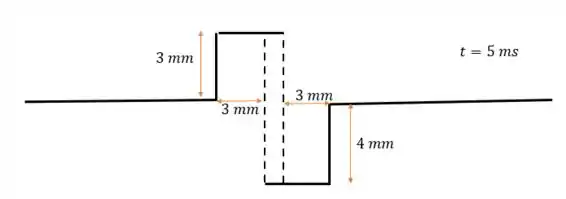
Na parte fora do pontilhado, não há interferência, então cada pulso segue sua vida normal
Mas dentro do pontilhado, temos uma interferência destrutiva, porque os pulsos vão se “cancelar”. Considerando como negativo o pulso que está pra baixo e positivo pra cima, a amplitude do pulso nessa região de vai ser:
Ou seja, amplitude de módulo igual a para baixo:
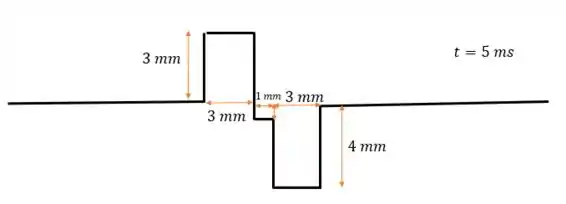
Passo 4
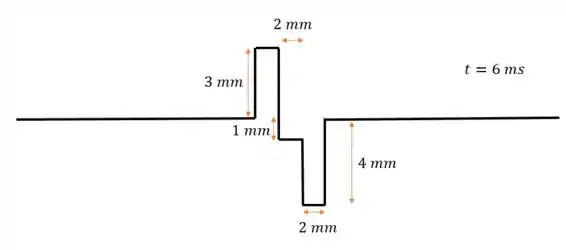
Em , o primeiro pulso vai ter se movido mais para a direita e o segundo mais para a esquerda (quando comparados ao desenho do passo 3), então:
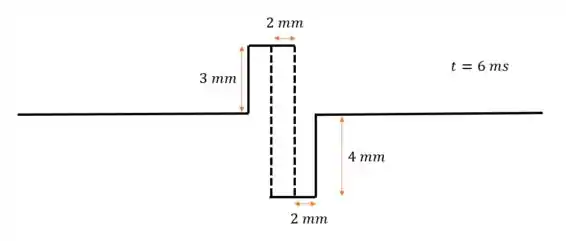
Na parte fora do pontilhado, não há interferência, então cada pulso segue sua vida normal
Mas dentro do pontilhado, temos uma interferência destrutiva, porque os pulsos vão se “cancelar”. Considerando como negativo o pulso que está pra baixo e positivo pra cima, a amplitude do pulso nessa região de vai ser:
Ou seja, amplitude de módulo igual a para baixo:
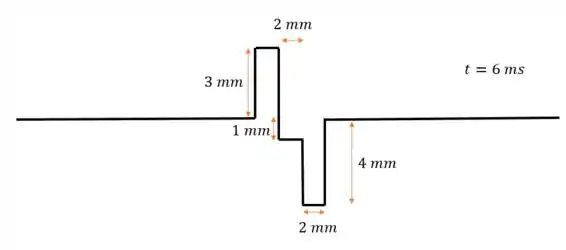
Passo 5
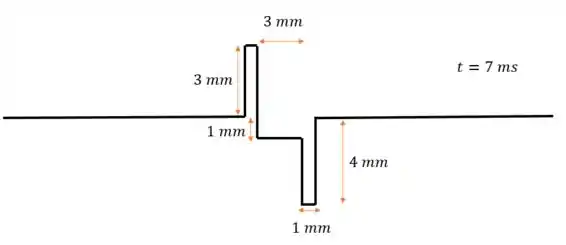
Em , o primeiro pulso vai ter se movido mais para a direita e o segundo mais para a esquerda (quando comparados ao desenho do passo 4), então:
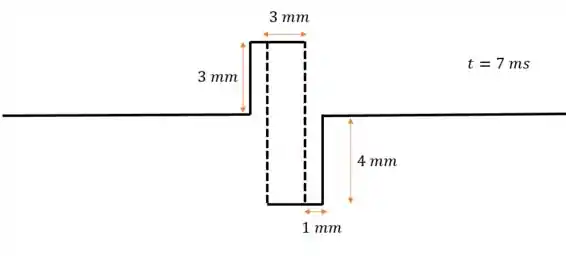
Na parte fora do pontilhado, não há interferência, então cada pulso segue sua vida normal
Mas dentro do pontilhado, temos uma interferência destrutiva, porque os pulsos vão se “cancelar”. Considerando como negativo o pulso que está pra baixo e positivo pra cima, a amplitude do pulso nessa região de vai ser:
Ou seja, amplitude de módulo igual a para baixo:
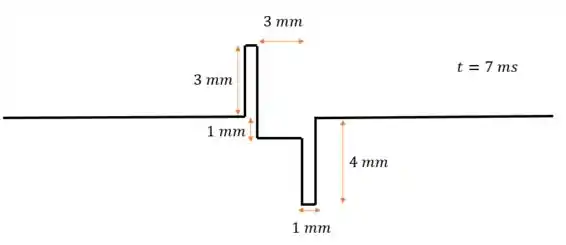
Passo 6
Em , o primeiro pulso vai ter se movido mais para a direita e o segundo mais para a esquerda (quando comparados ao desenho do passo 5), então:
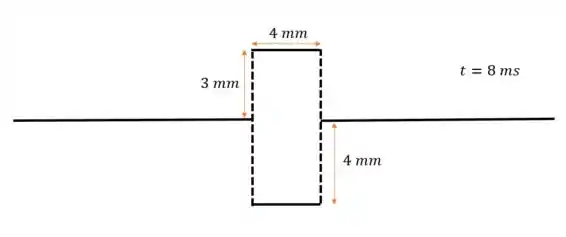
Na parte fora do pontilhado, não há interferência, então cada pulso segue sua vida normal
Mas dentro do pontilhado, temos uma interferência destrutiva, porque os pulsos vão se “cancelar”. Considerando como negativo o pulso que está pra baixo e positivo pra cima, a amplitude do pulso nessa região de vai ser:
Ou seja, amplitude de módulo igual a para baixo:
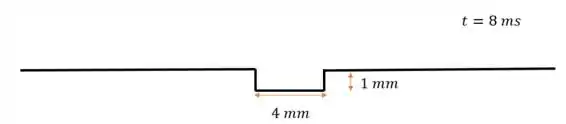
E isso acontece semelhantemente para , já que não temos mais a interação entre dois pulsos e o pulso restante continua viajando pela corda.
Resposta
