A figura mostra o ciclo a que é submetido de um gás ideal monoatômico. As temperaturas são , e . Para a trajetória , determine (a) o calor trocado , (b) a variação da energia interna e (c) o trabalho realizado . Para a trajetória , determine (d) , (e) e (f) . Para a trajetória , determine (g) , (h) e (i) . Para o ciclo completo, determine (j) , (k) e (l) . A pressão inicial no ponto é . Quais são (m) o volume e (n) a pressão no ponto e (o) o volume e (p) a pressão no ponto ?
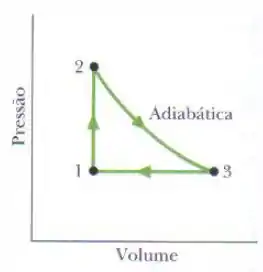
Passo 1
(a) Bom, na trajetória , o volume é constante, então pra calcular o valor trocado pelo gás, é só usar essa equação aqui:
E como o gás é monoatômico:
Substituindo os outros valores:
Passo 2
(b) Agora pra calcular a energia interna vamos usar a primeira lei da termodinâmica:
Como a trajetória acontece a volume constante, o trabalho é zero, e a energia interna é simplesmente o calor que acabamos de calcular:
Passo 3
(c) Como dito antes, o trabalho em uma transformação a volume constante é sempre zero. Então:
Passo 4
(d) Agora queremos o calor trocado pelo gás na trajetória , que segundo o enunciado é uma transformação adiabática.
Bom, uma transformação adiabática é justamente uma em que não existe troca de calor, portanto:
Passo 5
(e) Dessa vez, ao invés de usar a primeira lei da termodinâmica, vamos pela fórmula da variação de energia interna mesmo:
Passo 6
(f) Agora que já temos a variação da energia interna e o calor, é só usar a primeira lei da termodinâmica pra calcular o trabalho:
Passo 7
(g) Agora queremos a troca de calor na trajetória . Como essa é uma transformação a pressão constante, podemos usar essa fórmula aqui:
Passo 8
(h) Pra calcular a variação da energia interna podemos usar essa fórmula aqui:
Lembrando que é o calor específico molar a volume constante e que sempre será mesmo que o processo seja isobárico (o que muda do isobárico para o isovolumétrico é a fórmula do calor 😉)
Passo 9
(i) O trabalho pode ser calculado pela primeira lei da termodinâmica:
Passo 10
(j) O calor trocado no ciclo completo é simplesmente a soma de todos os calores que nós calculamos, ou seja:
Passo 11
(k) E a lógica da variação de energia interna é a mesma:
O que é esperado já que estamos falando de um ciclo completo.
Passo 12
(l) E o mesmo acontece para o trabalho total:
Passo 13
(m) Agora queremos o volume no ponto . A melhor forma de resolver isso é pegar algum ponto em que todas as grandezas sejam conhecidas, e comparar ele com o ponto pela lei dos gases ideais.
O ponto , por exemplo, serve pra isso. Nesse ponto o gás tem o mesmo volume que tem no ponto , então:
Passo 14
(n) E agora é só usar a outra formulação da lei dos gases ideais pra encontrar a pressão no ponto .
Podemos cortar os dois volumes, já que são iguais:
Passo 15
(o) Agora queremos o volume no ponto . É só usar a lei dos gases ideais:
A pressão é a mesma do ponto , que foi dada no enunciado, então:
Passo 16
(p) E pra finalizar, queremos a pressão nesse ponto, mas já até dissemos que é a mesma pressão do ponto , que já foi dada no enunciado:
Resposta
(a) .
(b) .
(c) .
(d) .
(e) .
(f) .
(g) .
(h) .
(i) .
(j) .
(k) .
(l) .
(m) .
(n) .
(o) .
(p) .