Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 19.Problemas Adicionais - Ex. 77
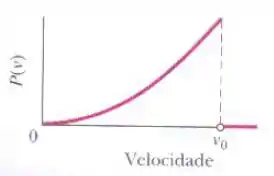
A figura mostra a distribuição hipotética de velocidades das partículas de um certo gás: para e para . Determine (a) uma expressão para em termos de , (b) a velocidade média das partículas e (c) a velocidade média quadrática das partículas.
Passo 1
(a) Sempre que você der de cara com uma distribuição de probabilidade, é muito provável (pelo menos nessa disciplina) que você precise usar essa propriedade aqui:
Que é basicamente o seguinte: a soma de todas as probabilidades é , nada muito surpreendente né?
Enfim, vamos usar isso pra procurar a “expressão” para em termos de :
No nosso caso, como a função é nula tanto antes do zero, quanto depois do , a gente pode trocar os limites de integração por esses valores:
Ótimo, conseguimos.
Passo 2
(b) A velocidade média das partículas é simplesmente o “valor esperado” dessa distribuição (talvez você lembre disso das aulas de estatística), a fórmula é essa aqui:
E jogando o valor de que acabamos de achar:
Passo 3
(c) A velocidade média quadrática também tem uma definição parecida:
E jogando o valor de que acabamos de achar:
Então:
Resposta
(a) .
(b) .
(c) .